High-precision newton-kantorovich method for nonlinear integral equations

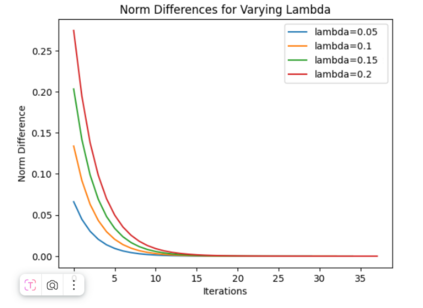
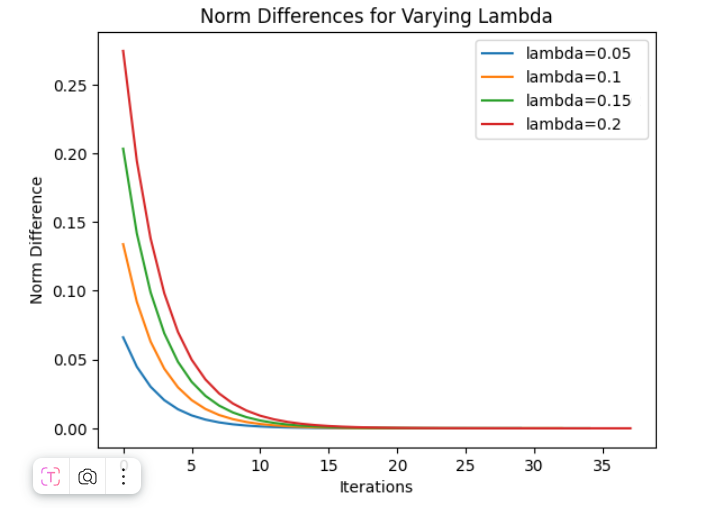
The paper considers the numerical solution of nonlinear integral equations using the Newton-Kantorovich method with the mpmath library. High-precision quadrature of the kernel K(t, s, u) with respect to the variable s for fixed t increases stability and accuracy in problems sensitive to rounding and dispersion. The presented implementation surpasses traditional low-precision methods, especially for strongly nonlinear kernels and stiff regimes, thereby expanding the applicability of the method in scientific and engineering computations.