Improved Bi-criteria Approximation for the All-or-Nothing Multicommodity Flow Problem in Arbitrary Networks

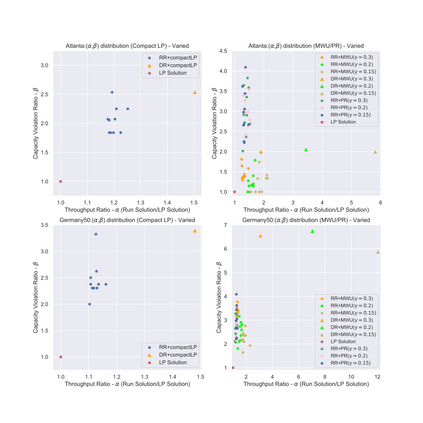
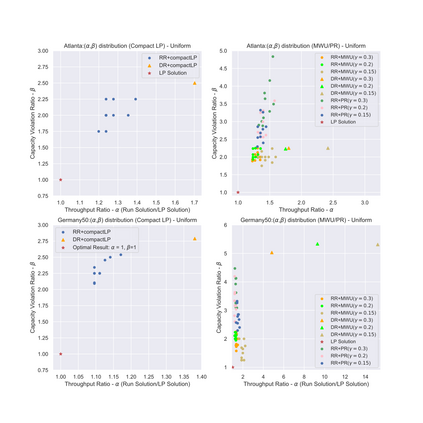
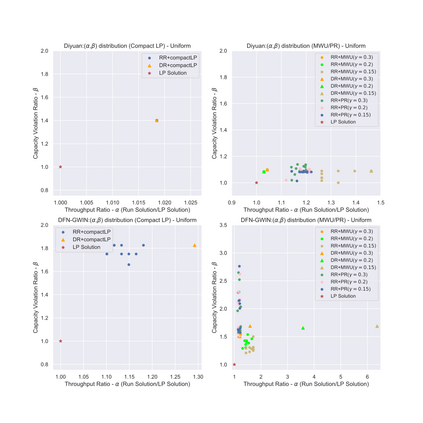
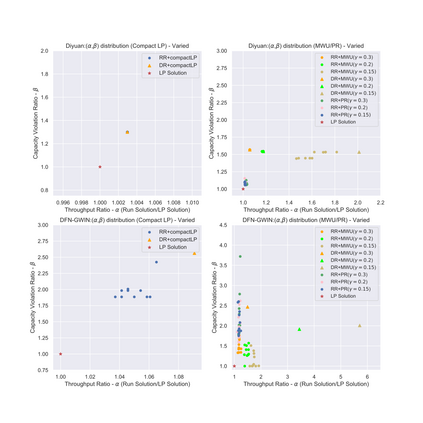
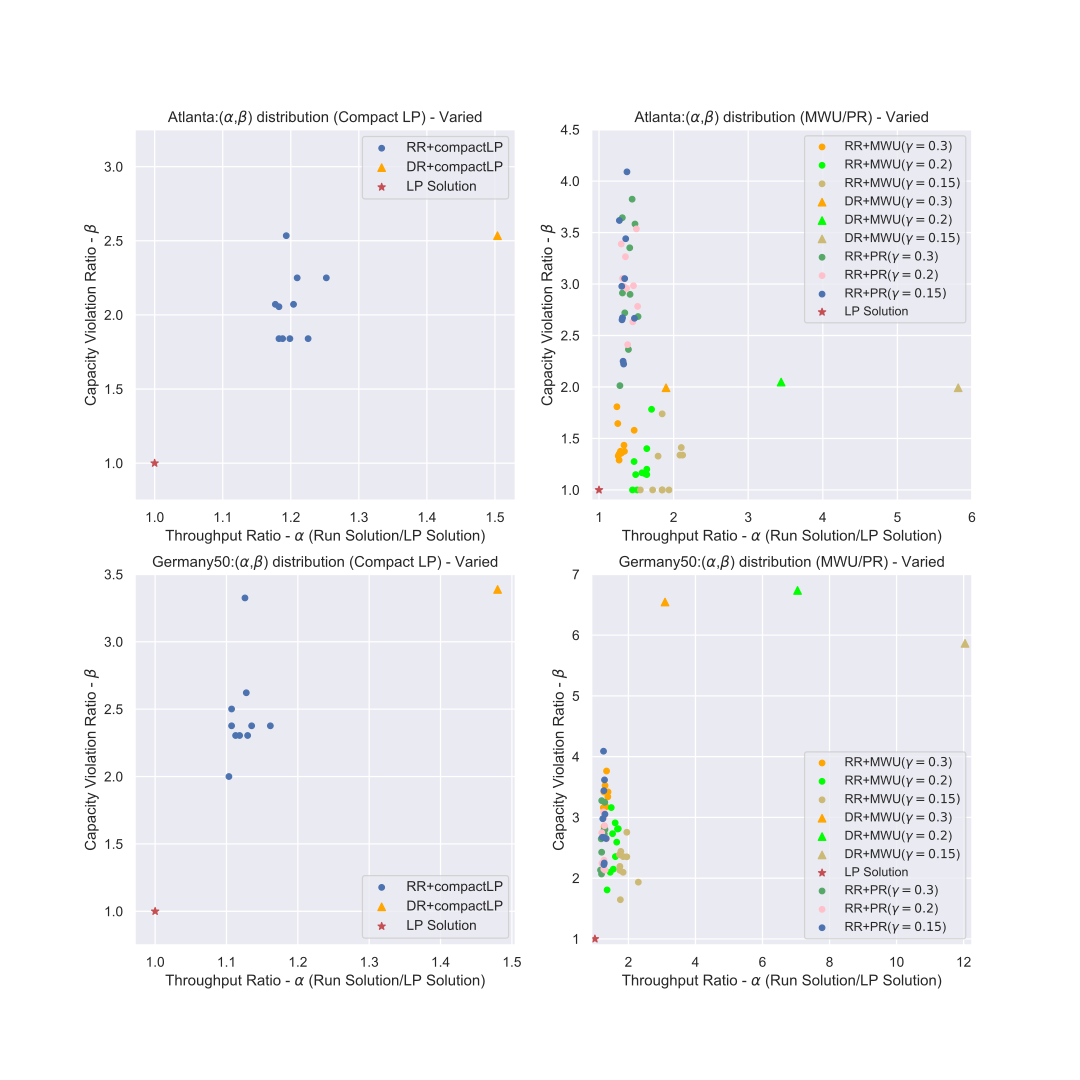
Throughput is a main performance objective in communication networks. This paper considers a fundamental maximum throughput routing problem -- the all-or-nothing multicommodity flow (ANF) problem -- in arbitrary directed graphs and in the practically relevant but challenging setting where demands can be (much) larger than the edge capacities. Hence, in addition to assigning requests to valid flows for each routed commodity, an admission control mechanism is required which prevents overloading the network when routing commodities. We make several contributions. On the theoretical side we obtain substantially improved bi-criteria approximation algorithms for this NP-hard problem. We present two non-trivial linear programming relaxations and show how to convert their fractional solutions into integer solutions via randomized rounding. One is an exponential-size formulation (solvable in polynomial time using a separation oracle) that considers a ``packing'' view and allows a more flexible approach, while the other is a generalization of the compact LP formulation of Liu et al. (INFOCOM'19) that allows for easy solving via standard LP solvers. We obtain a polynomial-time randomized algorithm that yields an arbitrarily good approximation on the weighted throughput while violating the edge capacity constraints by only a small multiplicative factor. We also describe a deterministic rounding algorithm by derandomization, using the method of pessimistic estimators. We complement our theoretical results with a proof of concept empirical evaluation.