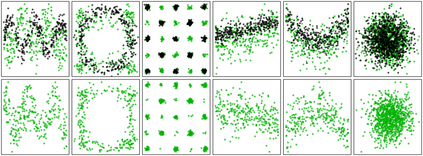
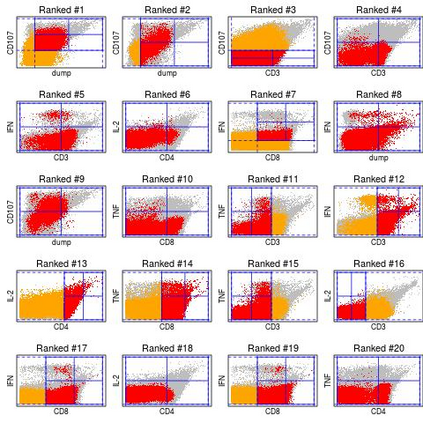
Identifying dependency in multivariate data is a common inference task that arises in numerous applications. However, existing nonparametric independence tests typically require computation that scales at least quadratically with the sample size, making it difficult to apply them to massive data. Moreover, resampling is usually necessary to evaluate the statistical significance of the resulting test statistics at finite sample sizes, further worsening the computational burden. We introduce a scalable, resampling-free approach to testing the independence between two random vectors by breaking down the task into simple univariate tests of independence on a collection of 2x2 contingency tables constructed through sequential coarse-to-fine discretization of the sample space, transforming the inference task into a multiple testing problem that can be completed with almost linear complexity with respect to the sample size. To address increasing dimensionality, we introduce a coarse-to-fine sequential adaptive procedure that exploits the spatial features of dependency structures to more effectively examine the sample space. We derive a finite-sample theory that guarantees the inferential validity of our adaptive procedure at any given sample size. In particular, we show that our approach can achieve strong control of the family-wise error rate without resampling or large-sample approximation. We demonstrate the substantial computational advantage of the procedure in comparison to existing approaches as well as its decent statistical power under various dependency scenarios through an extensive simulation study, and illustrate how the divide-and-conquer nature of the procedure can be exploited to not just test independence but to learn the nature of the underlying dependency. Finally, we demonstrate the use of our method through analyzing a large data set from a flow cytometry experiment.
翻译:在多种应用中,发现多变量数据的依赖性是一项常见的推论任务。然而,现有的非对称独立测试通常要求根据抽样面积的大小来计算比例,至少以四度为尺度,从而难以将其应用于大量数据。此外,通常需要重新取样,以评价由此得出的测试统计数据在有限的抽样规模中的统计意义,从而进一步加重计算负担。我们采用一种可缩放的、不复制的方法,通过将任务分成为简单的单向独立测试,检验两个随机矢量之间的独立性。然而,现有的非对称独立测试通常要求根据抽样空间的顺序粗向离散性来计算2x2应急表格,将推断任务转变为一个在抽样规模方面几乎线性复杂的多重测试问题。为了解决日益扩大的尺寸,我们引入了一种粗向线性排序的顺序调整程序,利用依赖结构的空间特征来更有效地检查样本空间。我们从一种保证我们适应程序在任何给定的样本大小上都具有更精确的自定义性,但从深度的自定义的自定义的自定义的自定义的自定义的自定义的自定义的自定义到自定义的自定义的自定义的自定义的自定义的自定义的自定义的自定义,特别,我们通过大量的自定义的自定义的自定义的自定义的自定义方法,我们从现有的、自定义的自定义的自定义的自定义的自定义的自定义的自定义的自定义的自定义的自定义的自定义的自定义的自定义的自定义的自定义,通过一个直观方法,通过一种自定义的自定义的自定义的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订方法,从订方法,通过一种自订的自订的自订的自订、自订方法,从订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的自订的