Synthesizing Inductive Lemmas for Reasoning with First-Order Logic with Least Fixpoints

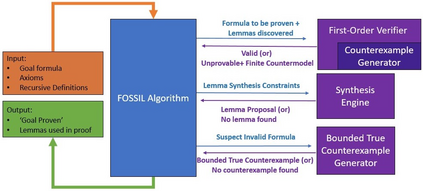
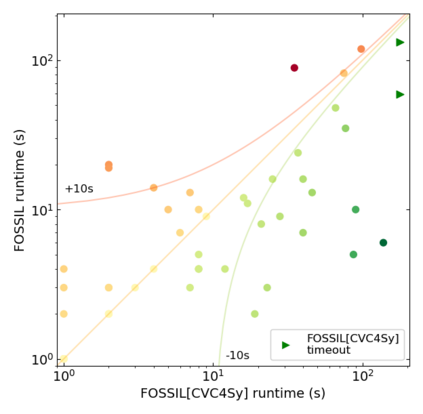
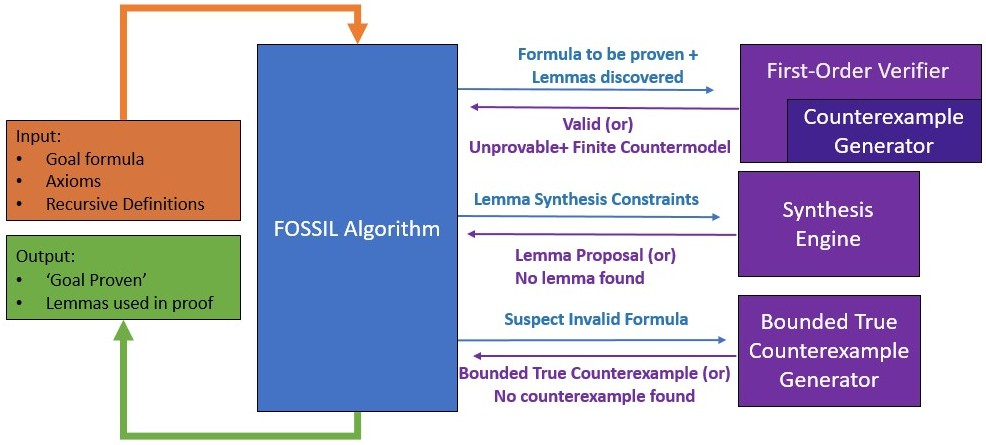
Recursively defined linked datastructures embedded in a pointer-based heap and their properties are naturally expressed in pure first-order logic with least fixpoint definitions (FO+lfp) combined with background theories. However, automated reasoning for such logics has not seen much progress. Such logics, unlike pure FOL, do not even admit complete procedures, let alone decidable ones. In this paper, we undertake a foundational study of automatically finding proofs that use induction to reason in these logics. By treating proofs as pure FO proofs that are punctuated by declarations of induction lemmas, we separate proofs into deductively reasoned components and statements of lemmas that need to be synthesized. While humans divine such lemmas with intuition, we propose a technique that guides the synthesis of such lemmas using counterexamples that are finite first-order models that witness the help required for proving a goal theorem as well as non-provability and invalidity of lemmas. We develop relatively complete procedures for synthesizing lemmas for powerful FO+lfp logics. We implement our procedures and evaluate them over a class of theorems involving heap datastructures that require inductive proofs.