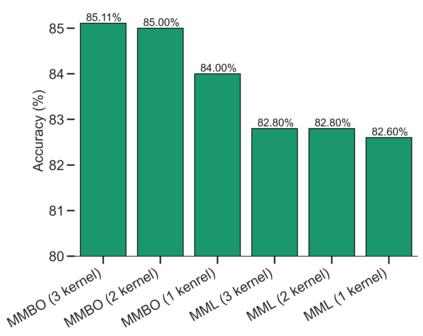
Machine learning methods have greatly changed science, engineering, finance, business, and other fields. Despite the tremendous accomplishments of machine learning and deep learning methods, many challenges still remain. In particular, the performance of machine learning methods is often severely affected in case of diverse data, usually associated with smaller data sets or data related to areas of study where the size of the data sets is constrained by the complexity and/or high cost of experiments. Moreover, data with limited labeled samples is a challenge to most learning approaches. In this paper, the aforementioned challenges are addressed by integrating graph-based frameworks, multiscale structure, modified and adapted optimization procedures and semi-supervised techniques. This results in two innovative multiscale Laplacian learning (MLL) approaches for machine learning tasks, such as data classification, and for tackling diverse data, data with limited samples and smaller data sets. The first approach, called multikernel manifold learning (MML), integrates manifold learning with multikernel information and solves a regularization problem consisting of a loss function and a warped kernel regularizer using multiscale graph Laplacians. The second approach, called the multiscale MBO (MMBO) method, introduces multiscale Laplacians to a modification of the famous classical Merriman-Bence-Osher (MBO) scheme, and makes use of fast solvers for finding the approximations to the extremal eigenvectors of the graph Laplacian. We demonstrate the performance of our methods experimentally on a variety of data sets, such as biological, text and image data, and compare them favorably to existing approaches.
翻译:机械学习方法在科学、工程、金融、商业和其他领域发生了巨大变化。尽管机器学习和深层次学习方法取得了巨大成就,但仍然存在许多挑战。特别是,机器学习方法的绩效往往在多种数据方面受到严重影响,这些数据通常与较小的数据集或与研究领域有关的数据有关,而这些领域的数据集或数据通常因复杂性和/或高成本而限制数据集的规模。此外,带有有限标签样本的数据是大多数学习方法的一个挑战。在本文中,上述挑战是通过综合基于图形的框架、多尺度结构、经修改和调整的优化程序和半监督技术等巨大的成就来解决的。这导致两种具有创新性的多尺度拉巴学习方法,例如数据分类,以及处理不同领域研究领域的数据,而这些领域的数据规模因复杂的和/或高成本而受到限制。第一种方法,即将多种内容的学习与多核心信息结合起来,并解决由损失功能和使用多尺度的平板块图的扭曲的图像调整器构成的正规化问题。第二种方法是,将多尺度的MBLLA-RO-S-C-S-Simal Syal Syal 方法称为多尺度的M-B-Syal-Syal-Syal-B-Syal-Syal-Syal-Syal-Syal-Syal-B-Syal-Syal-B-Sy-Sy-Sy-Sy-B-Syal-Sy-Syal-Sy-Sy-Sy-Sy-Sy-Sy-Sy-Syal-Syal-B-B-Syal-Sy-Syal-Sy-Sy-Sy-Syal-Sy-Sy-Sy-Sy-Sy-Sy-Sy-Sy-Sy-Sy-Sy-Sy-Sy-Sy-Sy-Sy-Sy-Sy-Sy-Sy-Sy-Sy-Sy-Sy-M-M-B-Sy-M-Sy-Sy-Sy-M-Sy-Sy-M-M-Sy-Sy-M-Sy-M-M-Sy-M-M-M-