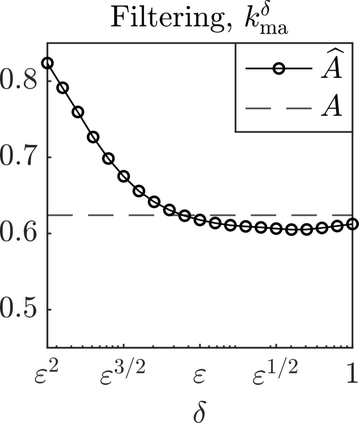
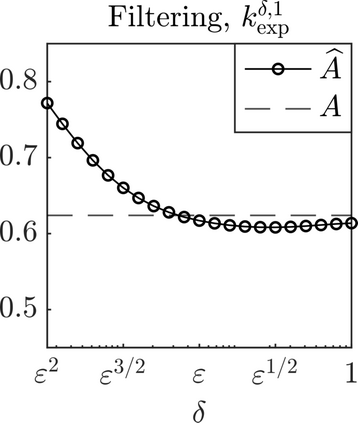
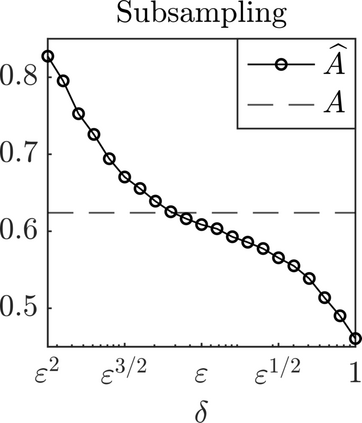
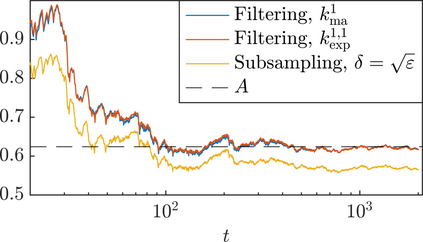
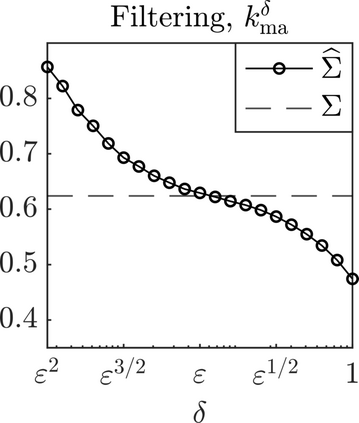
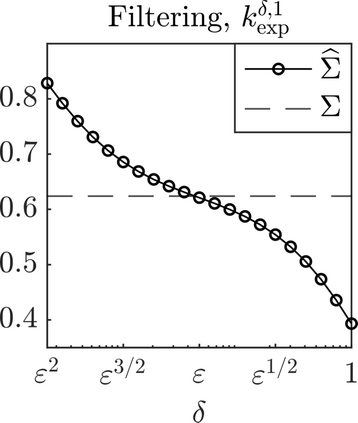
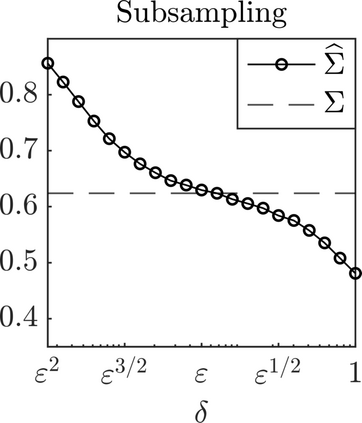
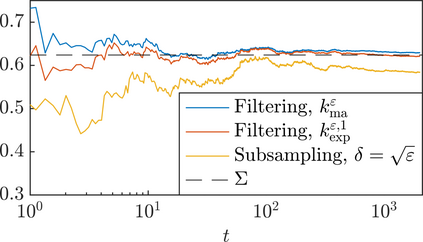
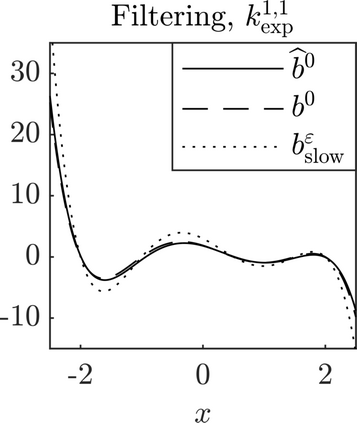
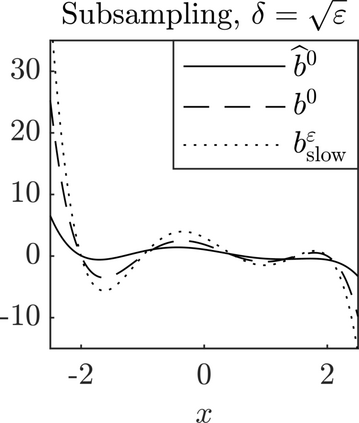
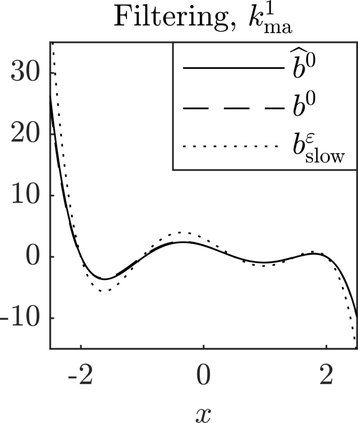
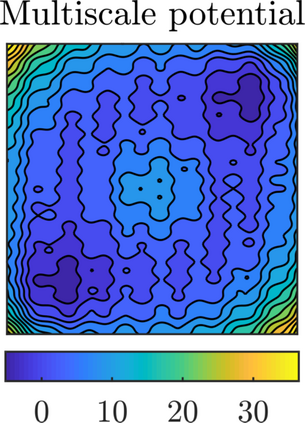
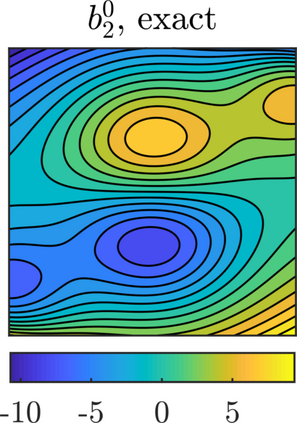
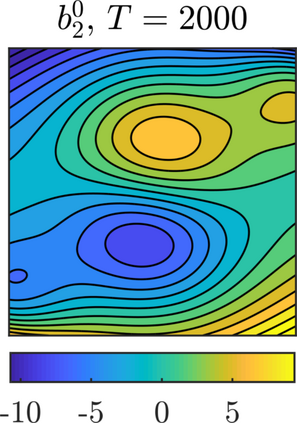
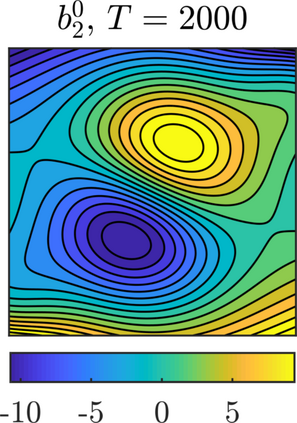
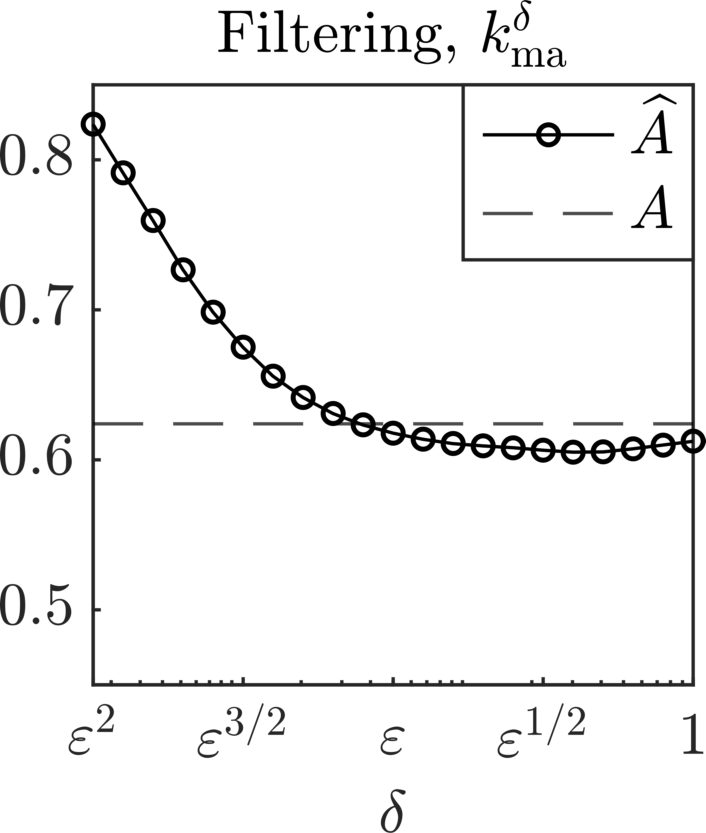
We present a methodology based on filtered data and moving averages for estimating robustly effective dynamics from observations of multiscale systems. We show in a semi-parametric framework of the Langevin type that the method we propose is asymptotically unbiased with respect to homogenization theory. Moreover, we demonstrate with a series of numerical experiments that the method we propose here outperforms traditional techniques for extracting coarse-grained dynamics from data, such as subsampling, in terms of bias and of robustness.
翻译:我们提出了一个基于过滤数据和移动平均数的方法,用于从多尺度系统的观测中估算稳健有效的动态。我们在Langevin类型的半参数框架中显示,我们建议的方法在同质化理论方面是无差别的。此外,我们用一系列数字实验来证明,我们在这里提出的方法在偏向和稳健方面超过了从数据中提取粗重重重力动态的传统技术,例如子抽样,在偏差和稳健性方面。
相关内容
专知会员服务
16+阅读 · 2019年11月30日
【变分推断课件】Lectures on Variational Inference: Approximate Bayesian Inference in Machine Learning(附带pdf)
专知会员服务
35+阅读 · 2019年11月30日
Arxiv
0+阅读 · 2021年10月28日
Arxiv
0+阅读 · 2021年10月27日
Arxiv
0+阅读 · 2021年10月25日