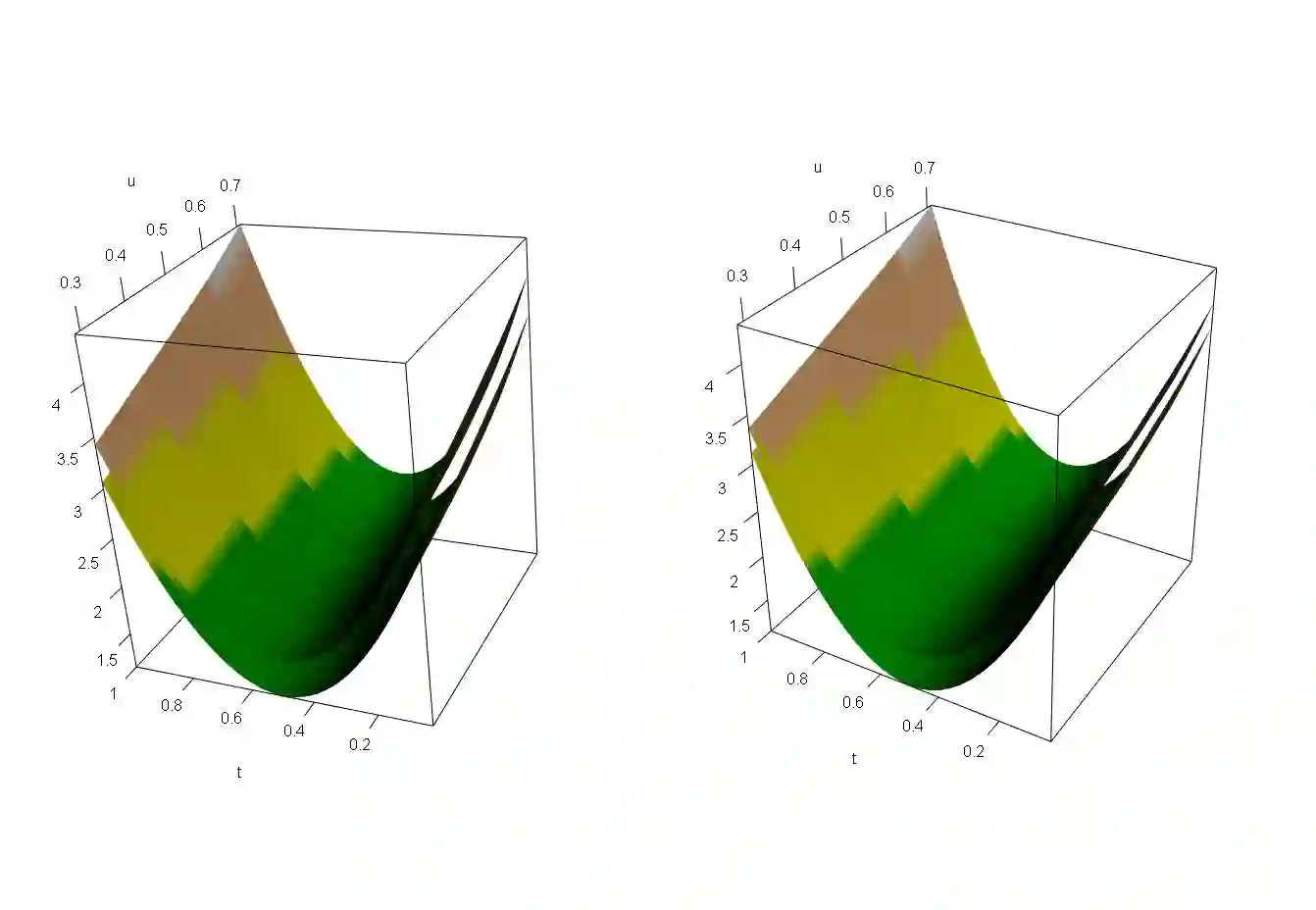
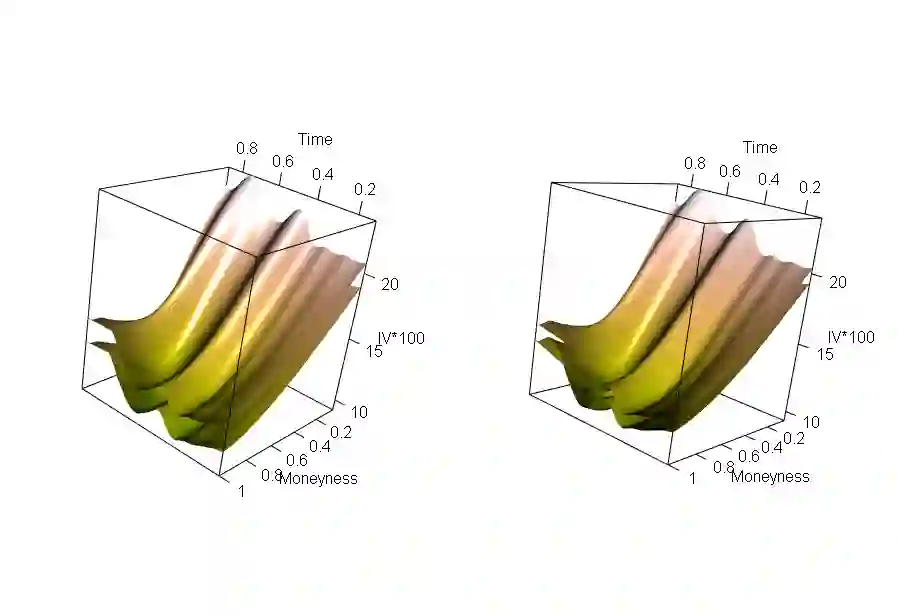
The problem of constructing a simultaneous confidence band for the mean function of a locally stationary functional time series $ \{ X_{i,n} (t) \}_{i = 1, \ldots, n}$ is challenging as these bands can not be built on classical limit theory. On the one hand, for a fixed argument $t$ of the functions $ X_{i,n}$, the maximum absolute deviation between an estimate and the time dependent regression function exhibits (after appropriate standardization) an extreme value behaviour with a Gumbel distribution in the limit. On the other hand, for stationary functional data, simultaneous confidence bands can be built on classical central theorems for Banach space valued random variables and the limit distribution of the maximum absolute deviation is given by the sup-norm of a Gaussian process. As both limit theorems have different rates of convergence, they are not compatible, and a weak convergence result, which could be used for the construction of a confidence surface in the locally stationary case, does not exist. In this paper we propose new bootstrap methodology to construct a simultaneous confidence band for the mean function of a locally stationary functional time series, which is motivated by a Gaussian approximation for the maximum absolute deviation. We prove the validity of our approach by asymptotic theory, demonstrate good finite sample properties by means of a simulation study and illustrate its applicability analyzing a data example.
翻译:为本地固定功能时间序列的平均值 $ ⁇ X ⁇ i,n} (t) ⁇ i = 1,\ldots, n} 问题在于如何为本地固定功能时间序列的平均值功能构建一个同时信任带。 因为这些频带不能建立在古典限理论上。 一方面, 对于固定参数的参数, $ X ⁇ i, n} 美元, 估计数和时间依赖回归函数显示之间的最大绝对偏差( 经过适当标准化后) 是一个极端值行为, 且在限制中分布 Gumbel 。 另一方面, 对于固定功能数据, 同步信任带可以建在Banach 空间的经典中央理论中, 随机变量值和最大绝对偏差的有限分布由高斯进程的一个顶点- 调来决定。 由于这两个参数的趋同率比率不同, 两者之间的最大绝对偏差是不兼容的, 而一个薄弱的趋同结果, 可用于在本地固定情况下构建信任面。 在本文中, 我们提出新的制套套套方法, 用来构建一个同时信任带, 用以构建Banach 随机偏差度的中, 通过一个具有最有动机的精确的精确的模型, 的模型, 的模型, 通过一个显示的精确的模型的精确性 来证明。