Neural networks-based backward scheme for fully nonlinear PDEs

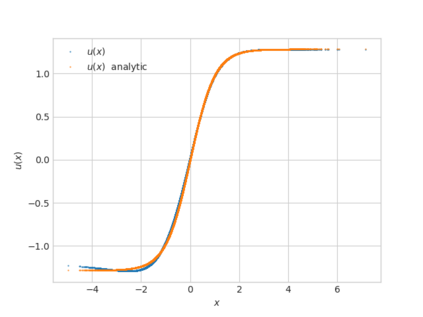
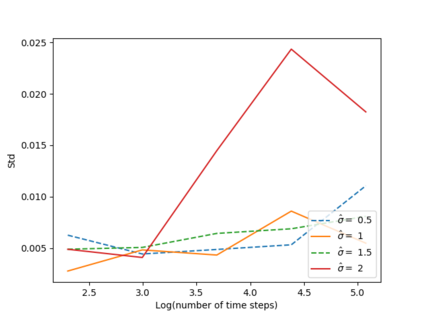
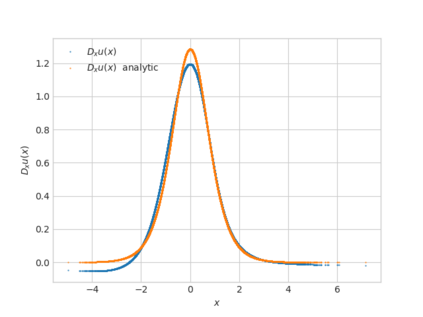
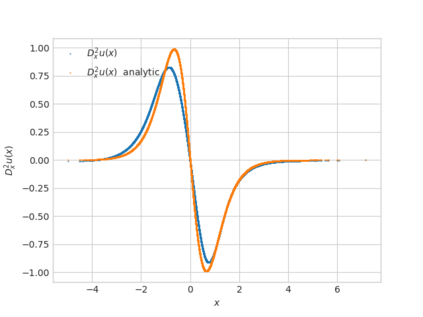
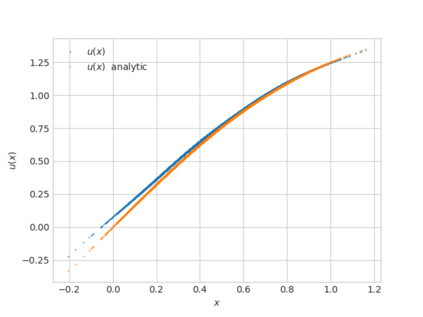
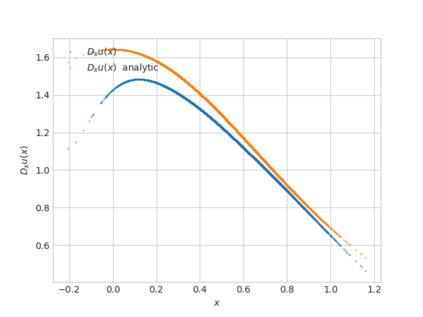
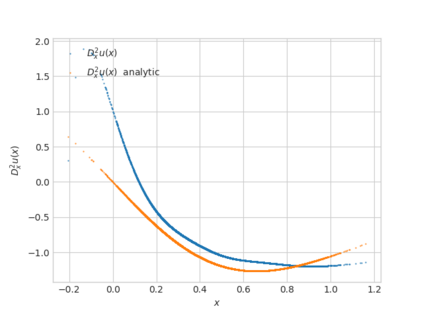
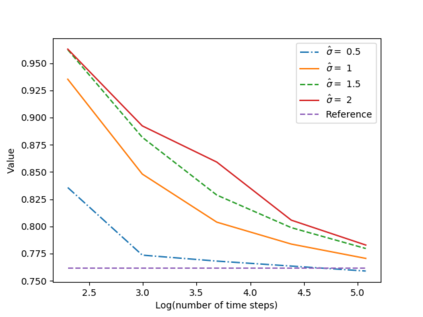
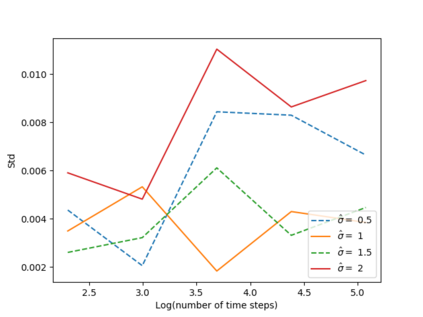
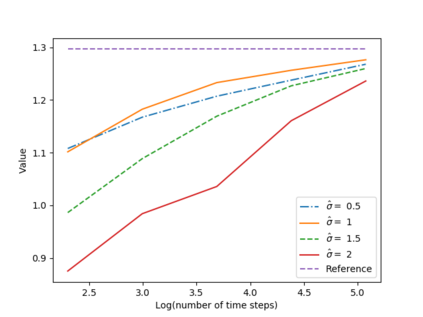
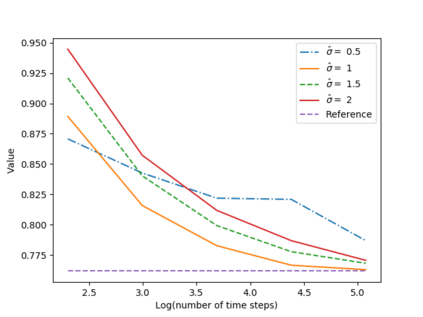
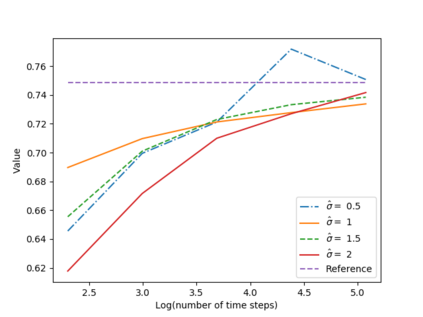
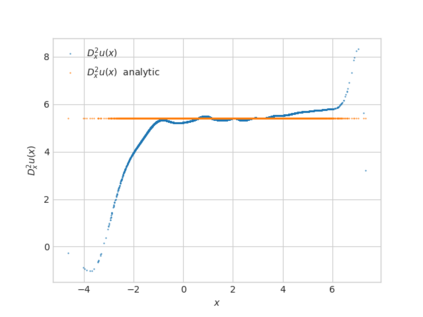
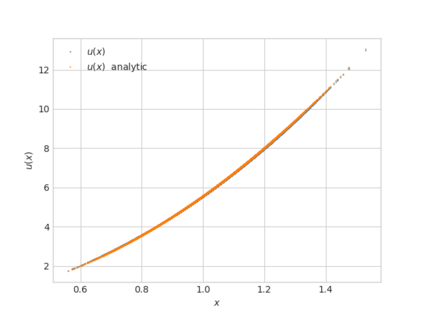
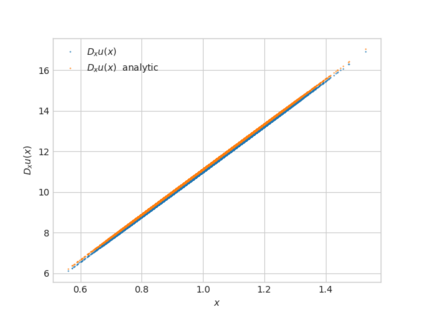
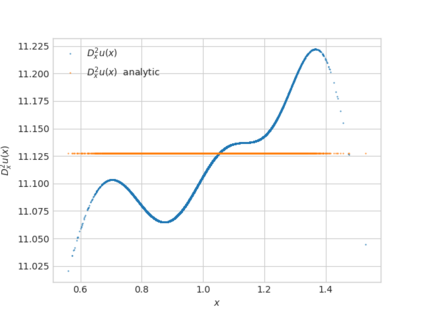
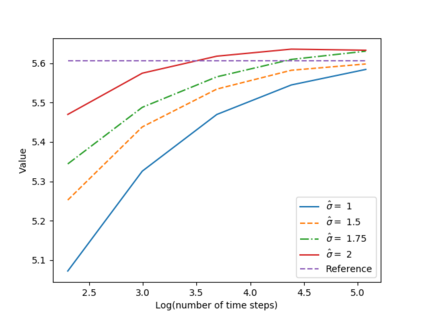
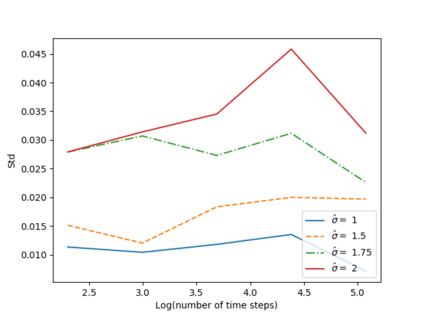
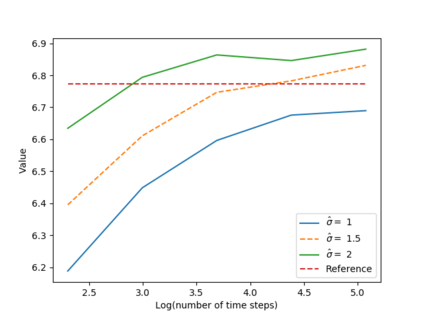
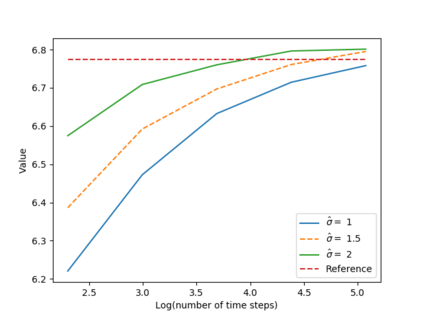
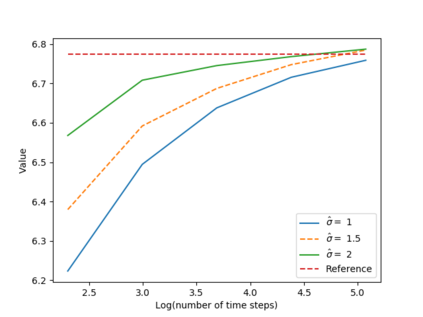
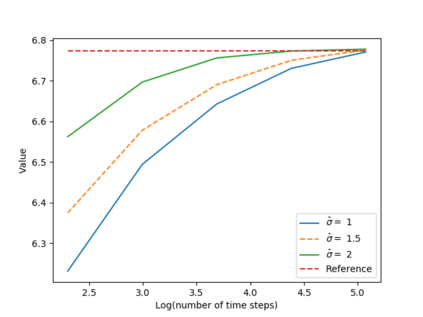
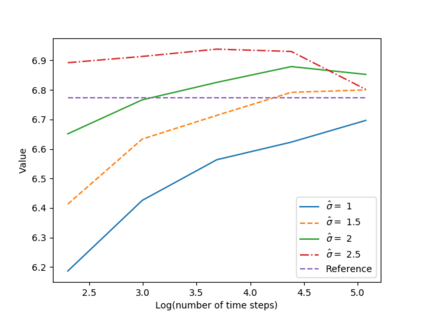
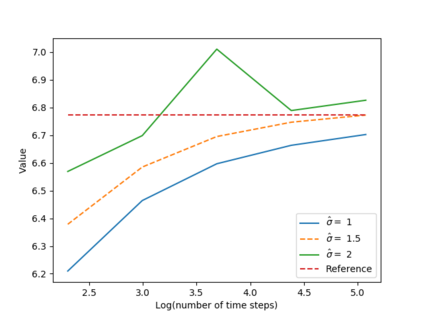
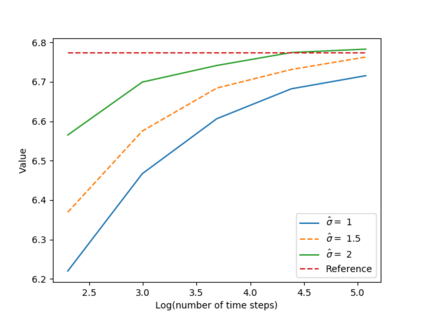
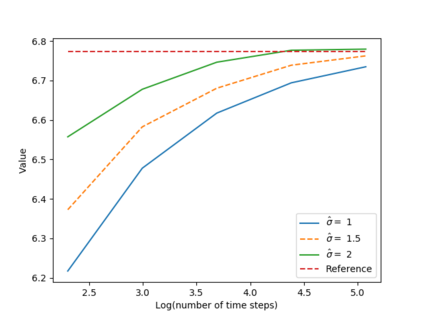
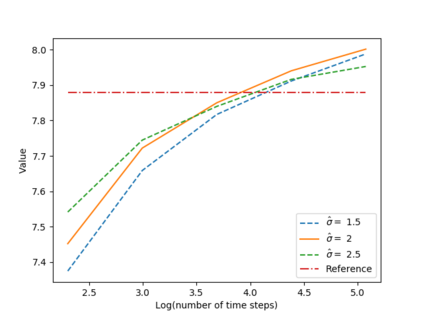
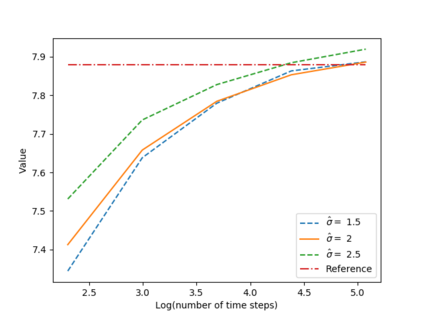
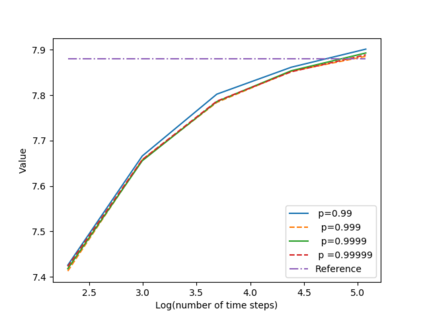
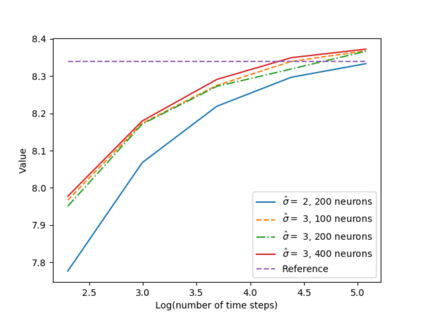
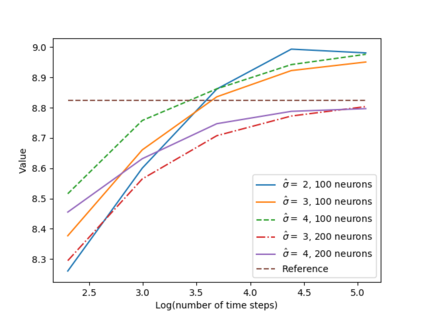
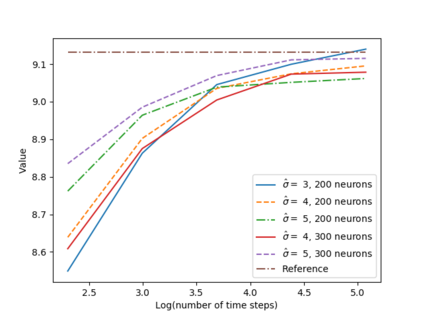
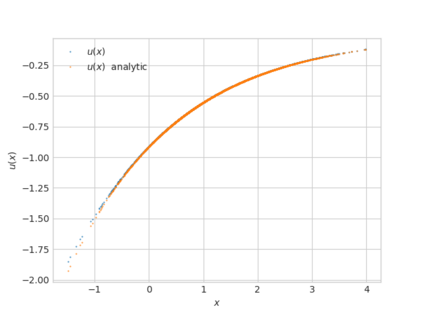
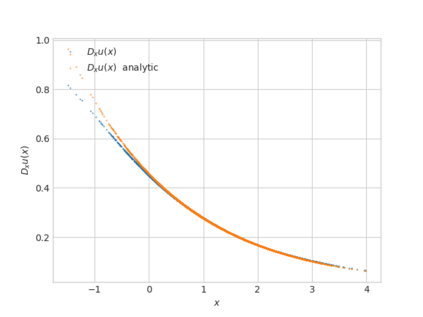
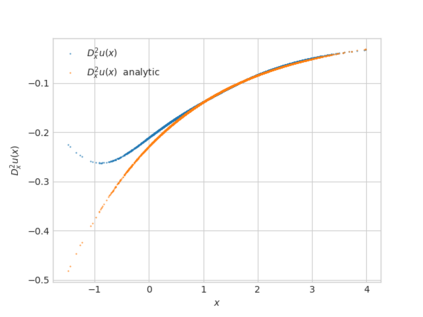
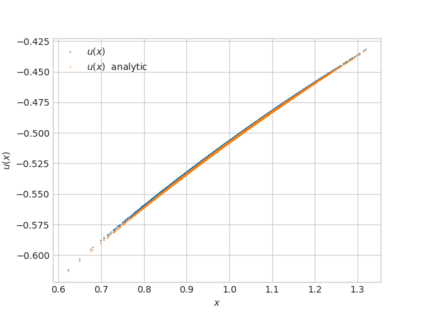
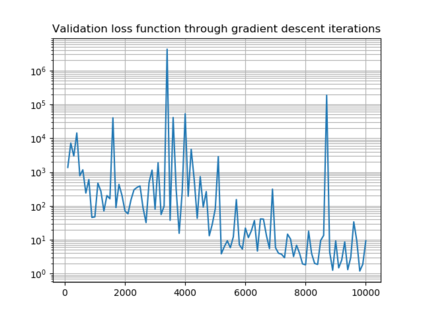
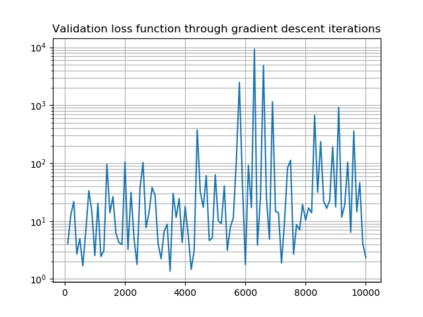
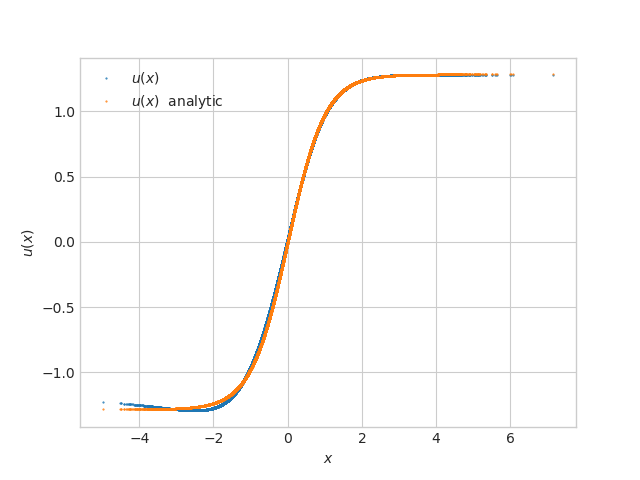
We propose a numerical method for solving high dimensional fully nonlinear partial differential equations (PDEs). Our algorithm estimates simultaneously by backward time induction the solution and its gradient by multi-layer neural networks, while the Hessian is approximated by automatic differentiation of the gradient at previous step. This methodology extends to the fully nonlinear case the approach recently proposed in \cite{HPW19} for semi-linear PDEs. Numerical tests illustrate the performance and accuracy of our method on several examples in high dimension with nonlinearity on the Hessian term including a linear quadratic control problem with control on the diffusion coefficient, Monge-Amp{\`e}re equation and Hamilton-Jacobi-Bellman equation in portfolio optimization.