DiffNet: Neural Field Solutions of Parametric Partial Differential Equations

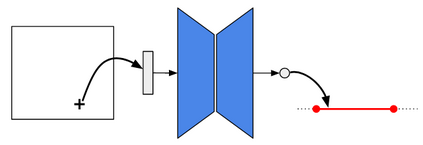
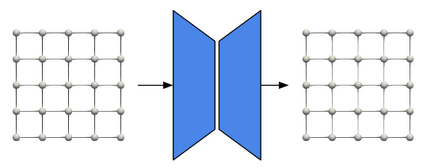
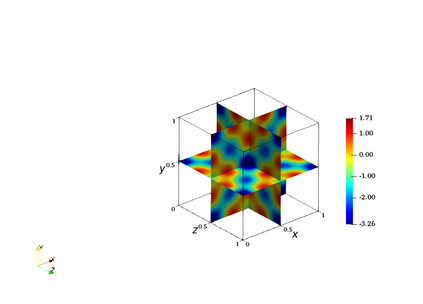
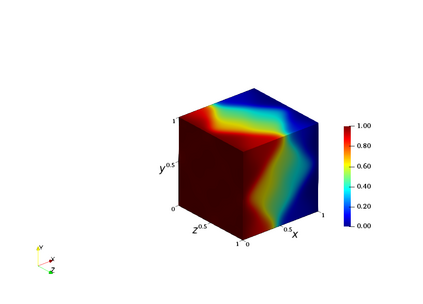
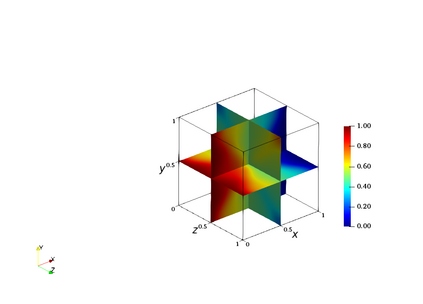
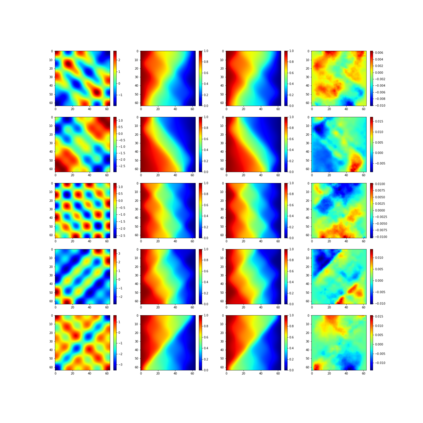
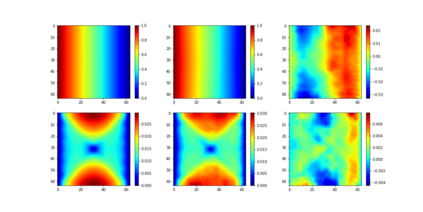
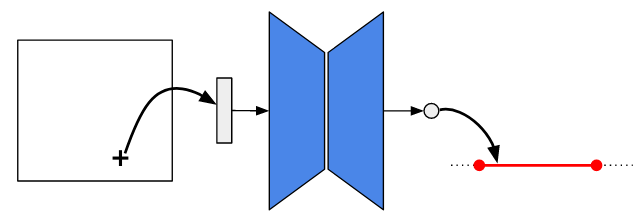
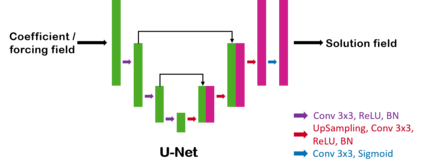We consider a mesh-based approach for training a neural network to produce field predictions of solutions to parametric partial differential equations (PDEs). This approach contrasts current approaches for ``neural PDE solvers'' that employ collocation-based methods to make point-wise predictions of solutions to PDEs. This approach has the advantage of naturally enforcing different boundary conditions as well as ease of invoking well-developed PDE theory -- including analysis of numerical stability and convergence -- to obtain capacity bounds for our proposed neural networks in discretized domains. We explore our mesh-based strategy, called DiffNet, using a weighted Galerkin loss function based on the Finite Element Method (FEM) on a parametric elliptic PDE. The weighted Galerkin loss (FEM loss) is similar to an energy functional that produces improved solutions, satisfies \textit{a priori} mesh convergence, and can model Dirichlet and Neumann boundary conditions. We prove theoretically, and illustrate with experiments, convergence results analogous to mesh convergence analysis deployed in finite element solutions to PDEs. These results suggest that a mesh-based neural network approach serves as a promising approach for solving parametric PDEs.