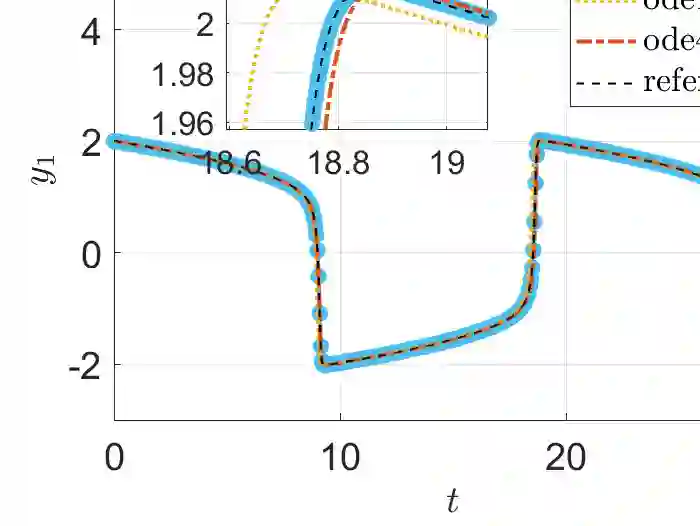
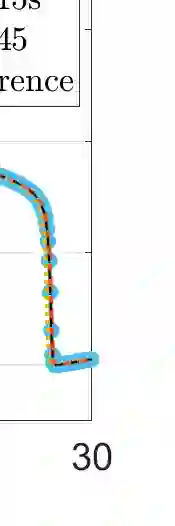
We propose a numerical method based on physics-informed Random Projection Neural Networks for the solution of Initial Value Problems (IVPs) of Ordinary Differential Equations (ODEs) with a focus on stiff problems. We address an Extreme Learning Machine with a single hidden layer with radial basis functions having as widths uniformly distributed random variables, while the values of the weights between the input and the hidden layer are set equal to one. The numerical solution of the IVPs is obtained by constructing a system of nonlinear algebraic equations, which is solved with respect to the output weights by the Gauss-Newton method, using a simple adaptive scheme for adjusting the time interval of integration. To assess its performance, we apply the proposed method for the solution of four benchmark stiff IVPs, namely the Prothero-Robinson, van der Pol, ROBER and HIRES problems. Our method is compared with an adaptive Runge-Kutta method based on the Dormand-Prince pair, and a variable-step variable-order multistep solver based on numerical differentiation formulas, as implemented in the \texttt{ode45} and \texttt{ode15s} MATLAB functions, respectively. We show that the proposed scheme yields good approximation accuracy, thus outperforming \texttt{ode45} and \texttt{ode15s}, especially in the cases where steep gradients arise. Furthermore, the computational times of our approach are comparable with those of the two MATLAB solvers for practical purposes.
翻译:我们提出一种基于物理知情随机随机投影神经网络的数值方法,以解决普通差异方程式初始值问题(IVPs) 的初始值问题,重点是棘手的问题。我们处理一个带有单一隐藏层的极端学习机,其半透明基函数以宽度统一分布随机变量,而输入层和隐藏层之间的权重数值被设定为等于一个。通过构建一个非线性代数方程式系统,获得IVP的数值解决方案,该方程式通过高尔斯-纽顿方法的输出权重来解决,使用一个简单的可比较性梯度调整整合时间间隔。为了评估其性能,我们应用了四个基准硬基IVP的解决方案的拟议方法,即Prothero-Robinson, van der Pol, ROBER 和 HIRRES 问题。我们的方法与一个适应性运行-Kutta 方法进行了比较,该方法通过高尔曼-Princal 方程式的可变式二级AB级求求求求求求求求解。 以数字公式为基础, 具体地计算公式中的正值=正正值=正值, 方向的正值=正值函数。