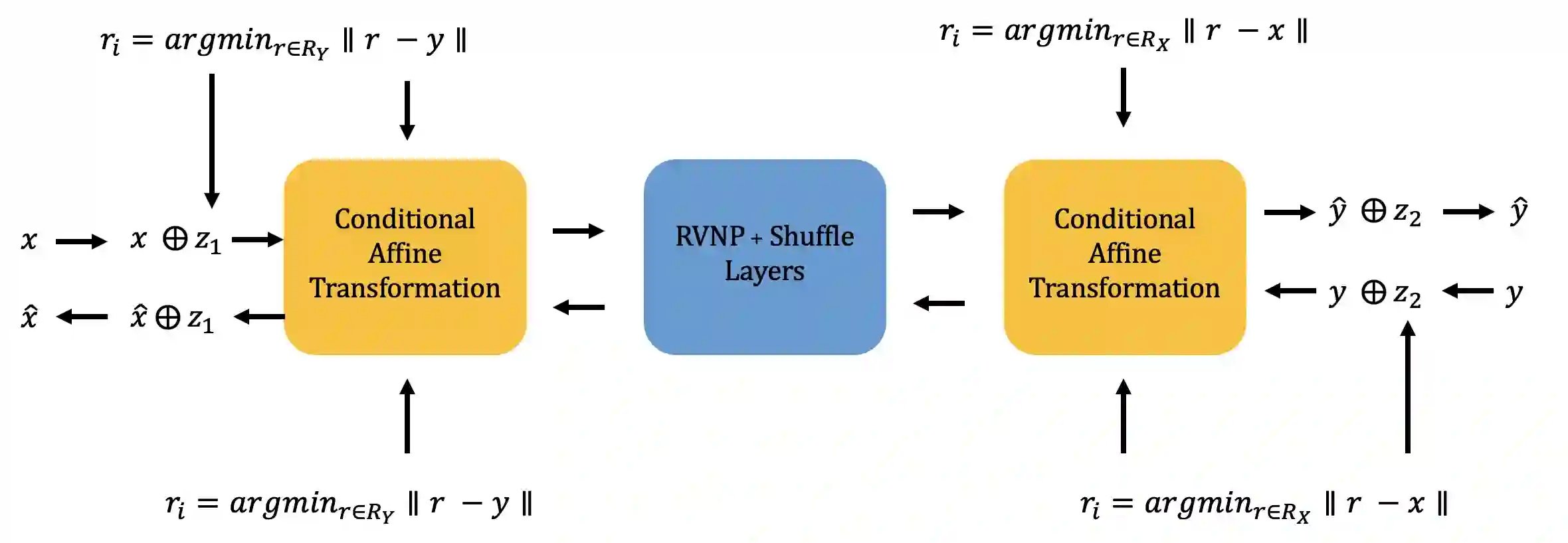
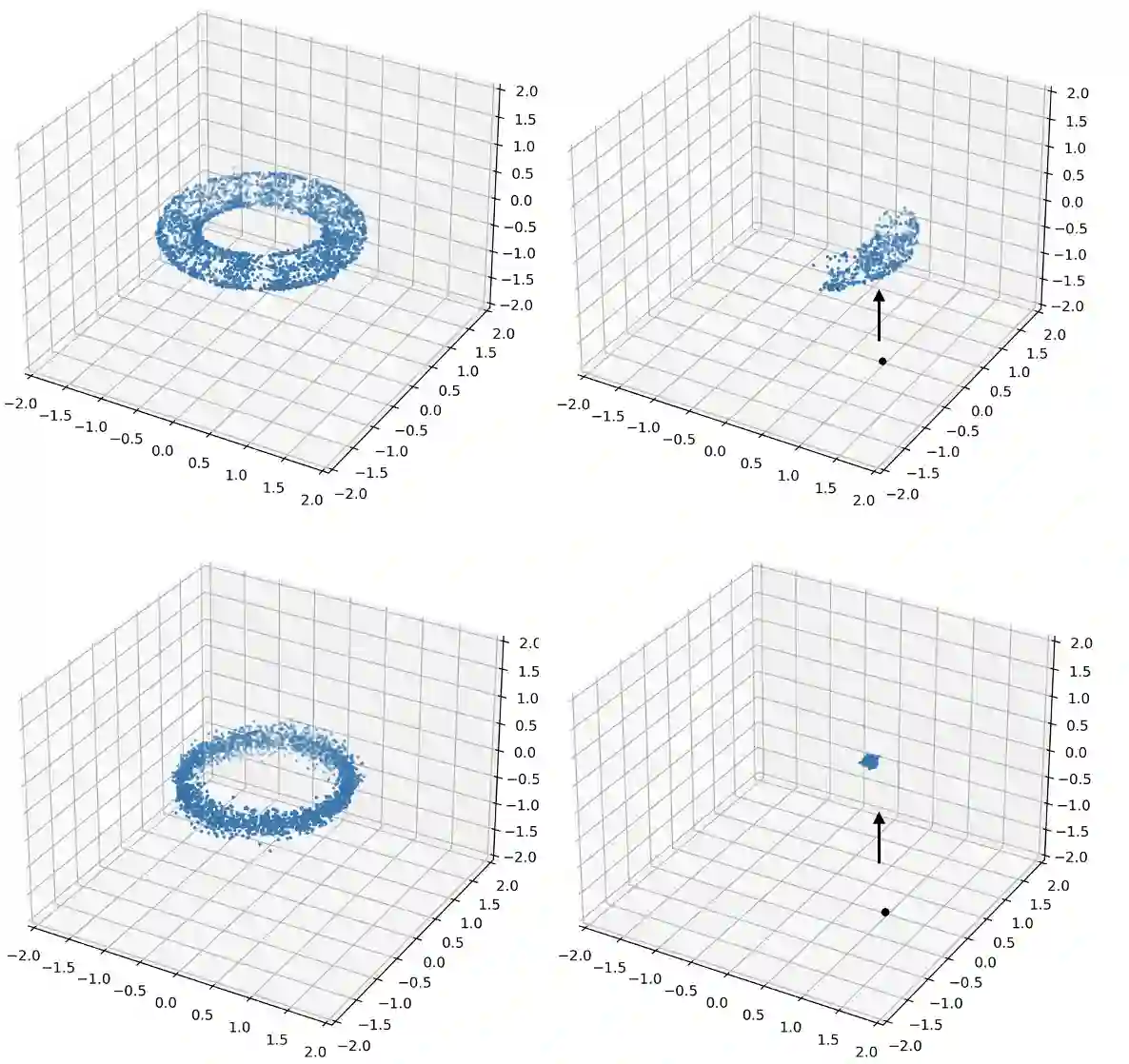
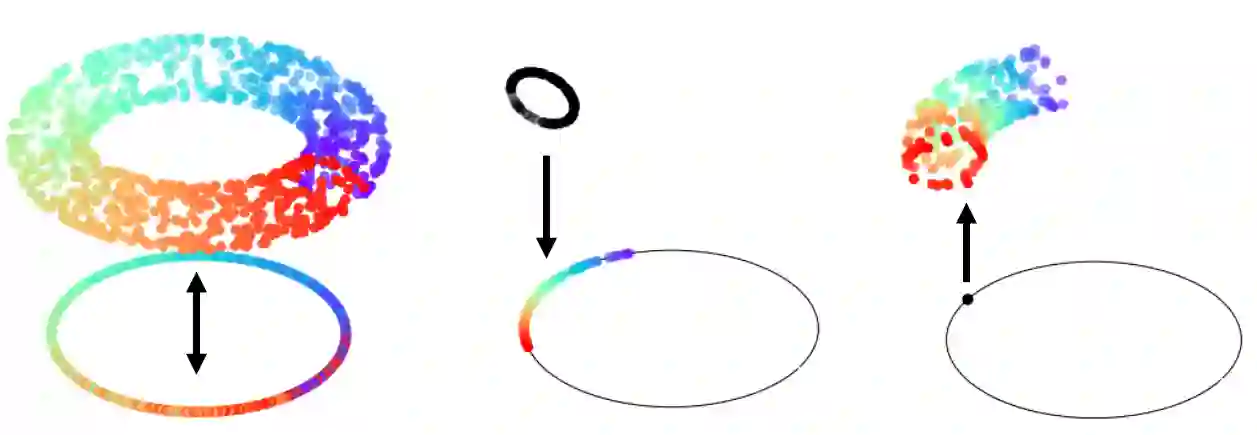
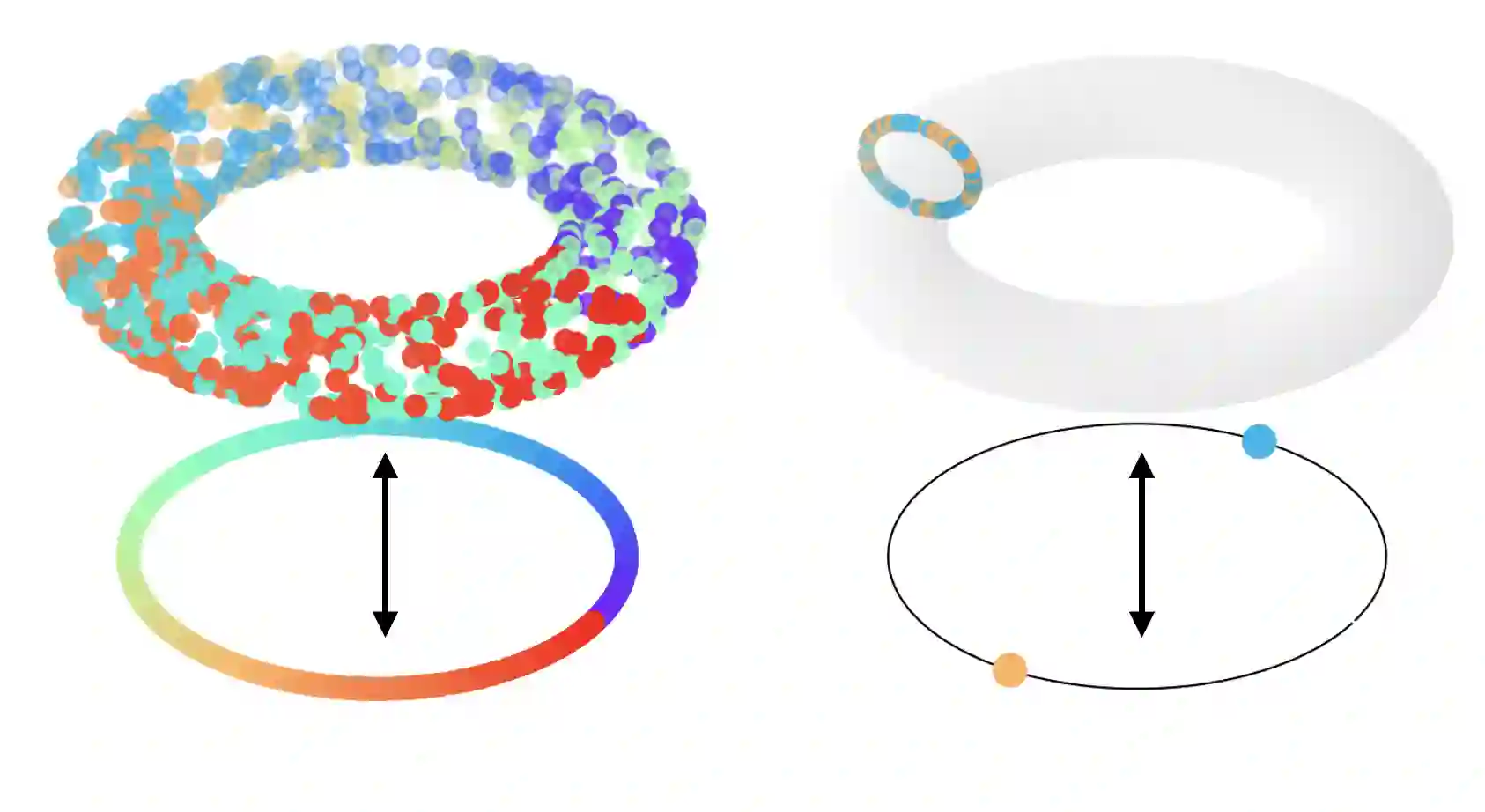
While it is not generally reflected in the `nice' datasets used for benchmarking machine learning algorithms, the real-world is full of processes that would be best described as many-to-many. That is, a single input can potentially yield many different outputs (whether due to noise, imperfect measurement, or intrinsic stochasticity in the process) and many different inputs can yield the same output (that is, the map is not injective). For example, imagine a sentiment analysis task where, due to linguistic ambiguity, a single statement can have a range of different sentiment interpretations while at the same time many distinct statements can represent the same sentiment. When modeling such a multivalued function $f: X \rightarrow Y$, it is frequently useful to be able to model the distribution on $f(x)$ for specific input $x$ as well as the distribution on fiber $f^{-1}(y)$ for specific output $y$. Such an analysis helps the user (i) better understand the variance intrinsic to the process they are studying and (ii) understand the range of specific input $x$ that can be used to achieve output $y$. Following existing work which used a fiber bundle framework to better model many-to-one processes, we describe how morphisms of fiber bundles provide a template for building models which naturally capture the structure of many-to-many processes.
翻译:虽然它一般没有反映在用于制定机器学习算法基准的“精度”数据集中,但现实世界充满了各种进程,这些进程最好被描述为多到多的过程。也就是说,单一输入有可能产生许多不同的产出(无论是由于噪音、不完善的测量或过程内在的随机性),而许多不同的输入可以产生相同的产出(即地图不是预测值)。例如,想象一种情绪分析任务,在这种任务中,由于语言模糊,一个单一的语句可以产生一系列不同的情绪解释,而同时许多不同的语句可以代表同样的情绪。当模拟这种多值函数时:X\rightrow Y$,通常能够用美元(x)来模拟具体投入的分布,以及用纤维($ ⁇ -1}(y)来分配具体产出美元。这种分析有助于用户(i)更好地了解他们正在研究的过程所固有的差异,以及(ii)了解具体输入的美元(xy)的范围。当模拟这种输入可以用来更好地描述我们用来实现成金模格式的模型的模型时,我们经常需要用一个更好的模型来描述一个更好的模型。