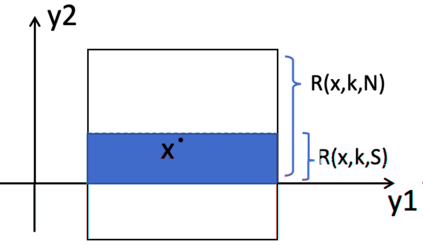
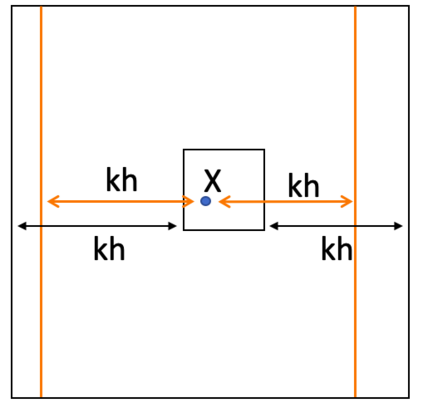
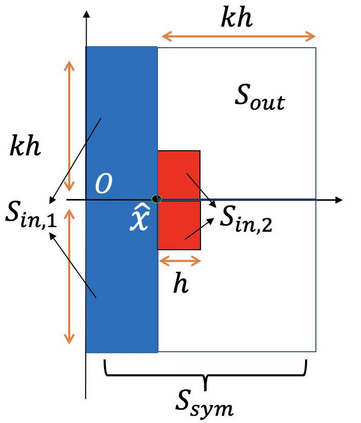
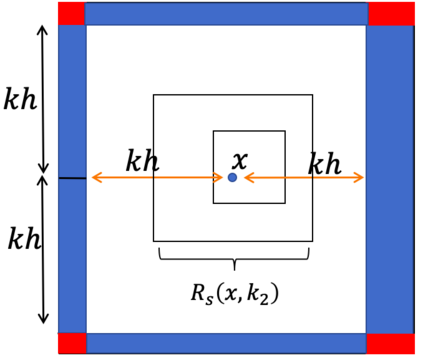
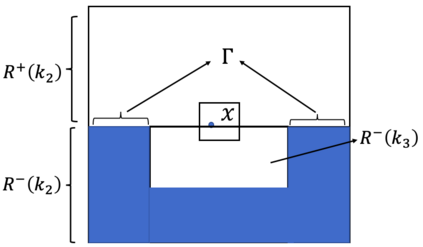
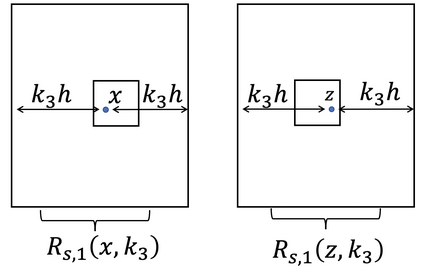
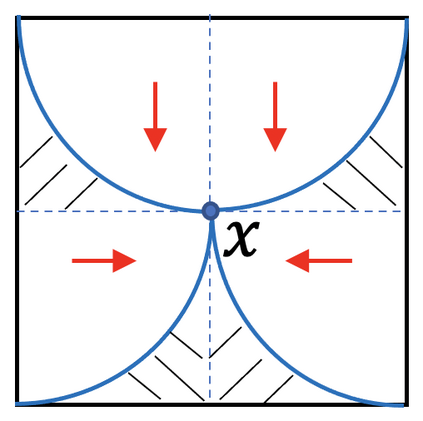
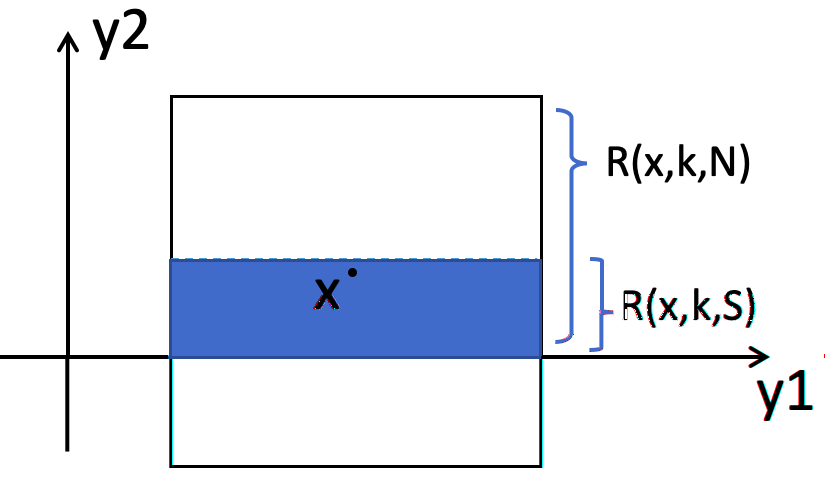
This is Part II of our paper in which we prove finite time blowup of the 2D Boussinesq and 3D axisymmetric Euler equations with smooth initial data of finite energy and boundary. In Part I of our paper [ChenHou2023a], we establish an analytic framework to prove stability of an approximate self-similar blowup profile by a combination of a weighted $L^\infty$ norm and a weighted $C^{1/2}$ norm. Under the assumption that the stability constants, which depend on the approximate steady state, satisfy certain inequalities stated in our stability lemma, we prove stable nearly self-similar blowup of the 2D Boussinesq and 3D Euler equations with smooth initial data and boundary. In Part II of our paper, we provide sharp stability estimates of the linearized operator by constructing space-time solutions with rigorous error control. We also obtain sharp estimates of the velocity in the regular case using computer assistance. These results enable us to verify that the stability constants obtained in Part I [ChenHou2023a] indeed satisfy the inequalities in our stability lemma. This completes the analysis of the finite time singularity of the axisymmetric Euler equations with smooth initial data and boundary.
翻译:暂无翻译