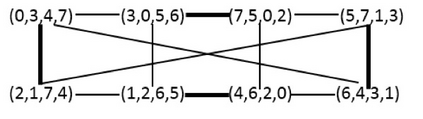
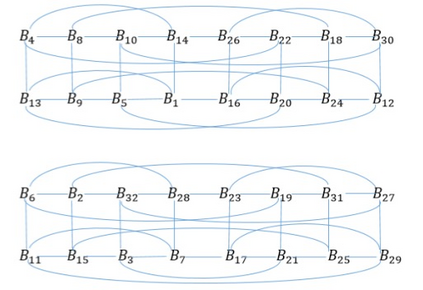
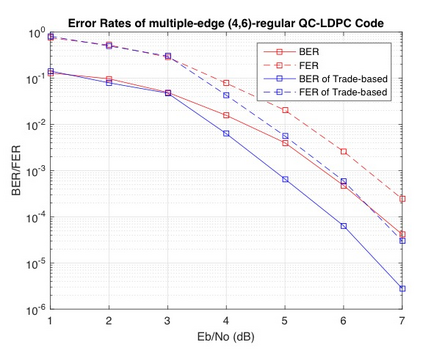
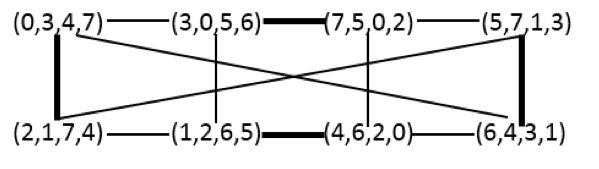
LDPC codes based on multiple-edge protographs potentially have larger minimum distances compared to their counterparts, single-edge protographs. However, considering different features of their Tanner graph, such as short cycles, girth and other graphical structures, is harder than for Tanner graphs from single-edge protographs. In this paper, we provide a novel approach to construct the parity-check matrix of an LDPC code which is based on trades obtained from block designs. We employ our method to construct two important categories of LDPC codes; quasi-cyclic (QC) LDPC and spatially-coupled LDPC (SC-LDPC) codes. We use those trade-based matrices to define base matrices of multiple-edge protographs. The construction of exponent matrices corresponding to these base matrices has less complexity compared to the ones proposed in the literature. We prove that these base matrices result in QC-LDPC codes with smaller lower bounds on the lifting degree than existing ones. There are three categories of SC-LDPC codes: periodic, time-invariant and time-varying. Constructing the parity-check matrix of the third one is more difficult because of the time dependency in the parity-check matrix. We use a trade-based matrix to obtain the parity-check matrix of a time-varying SC-LDPC code in which each downwards row displacement of the trade-based matrix yields syndrome matrices of a particular time. Combining the different row shifts the whole parity-check matrix is obtained. Our proposed method to construct parity-check and base matrices from trade designs is applicable to any type of super-simple directed block designs. We apply our technique to directed designs with smallest defining sets containing at least half of the blocks. To demonstrate the significance of our contribution, we provide a number of numerical and simulation results.
翻译:以多端编程制成的LDPC代码可能比对等方(单端编程)的距离最小,但考虑到其坦纳图的不同特征,如短周期、长环和其他图形结构,比对坦纳图的单端编程图要难。在本文中,我们提供了一种新颖的方法,用于构建基于区块设计交易的LDPC代码的对等检查矩阵。我们使用我们的方法,构建了两种重要的LDPC代码;准周期(QC)LDPC)和空间相联的LDPC(SC-LDPC)代码。我们使用这些基于贸易图的基于贸易的基于贸易基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数。获得的SC-LDPC代码分为三类:定期、时间差差最小基数基数基数基数基数基数基数基数基数基数基数的基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数的对比比数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数的对基数基数基数基数基数基数基数基数基数基数基数基数基数基数基数的对基数基数基数基数基数的对基数的对基数。我们基数的对基数基数基数基数基数基数的对基数基数基数基数基数基数基数基数基数的对基数的对基数基数基数基数基数基数的对基数基数的对基数的对基数基数基数基数的对基数基数基数的对基数的对基数的对基数的对基数的对基数的对基数的对基数基数基数基数的对基数基数基数基数基数基数的对基数的对基