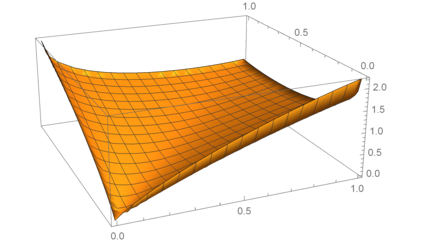
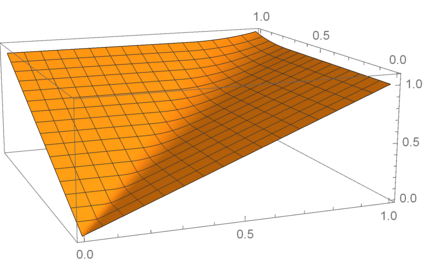
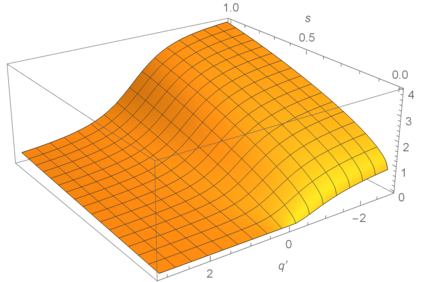
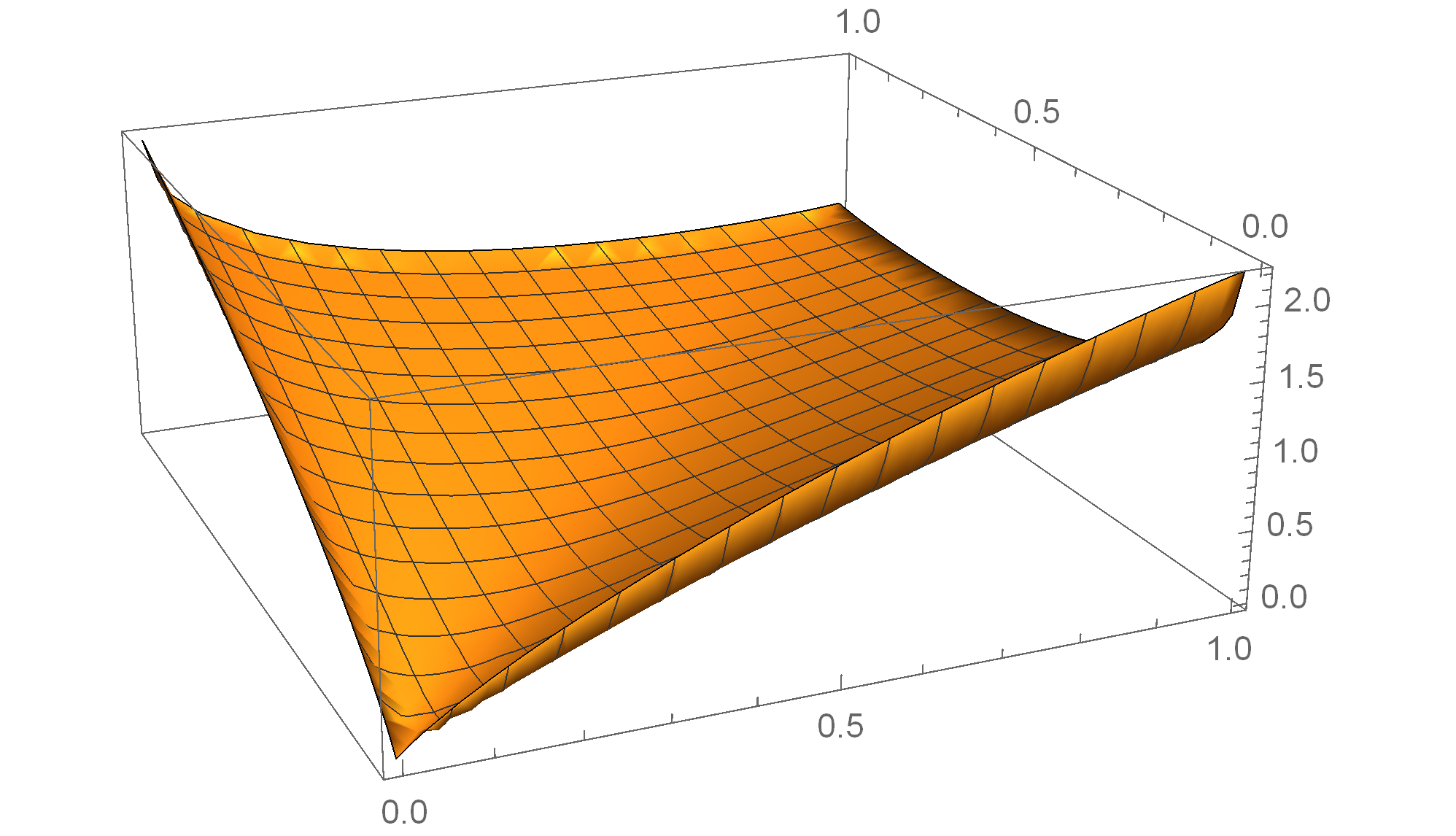
In this paper, we prove that for the doubly symmetric binary distribution, the lower increasing envelope and the upper envelope of the minimum-relative-entropy region are respectively convex and concave. We also prove that another function induced the minimum-relative-entropy region is concave. These two envelopes and this function were previously used to characterize the optimal exponents in strong small-set expansion problems and strong Brascamp--Lieb inequalities. The results in this paper, combined with the strong small-set expansion theorem derived by Yu, Anantharam, and Chen (2021), and the strong Brascamp--Lieb inequality derived by Yu (2021), confirm positively Ordentlich--Polyanskiy--Shayevitz's conjecture on the strong small-set expansion (2019) and Polyanskiy's conjecture on the strong Brascamp--Lieb inequality (2016). The proofs in this paper are based on the equivalence between the convexity of a function and the convexity of the set of minimizers of its Lagrangian dual.
翻译:在本文中,我们证明,对于双对称二进制分布,最小对称-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对流-对等-对等-对等-对等-对等-对等-对等-对等-对准-对等-对准-对准-对准-对准-对准-对准-对准-对准-对准-对准-对准-对准-对准-对准-对等-对准-对准-对准-对准-对准-对准-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对-对