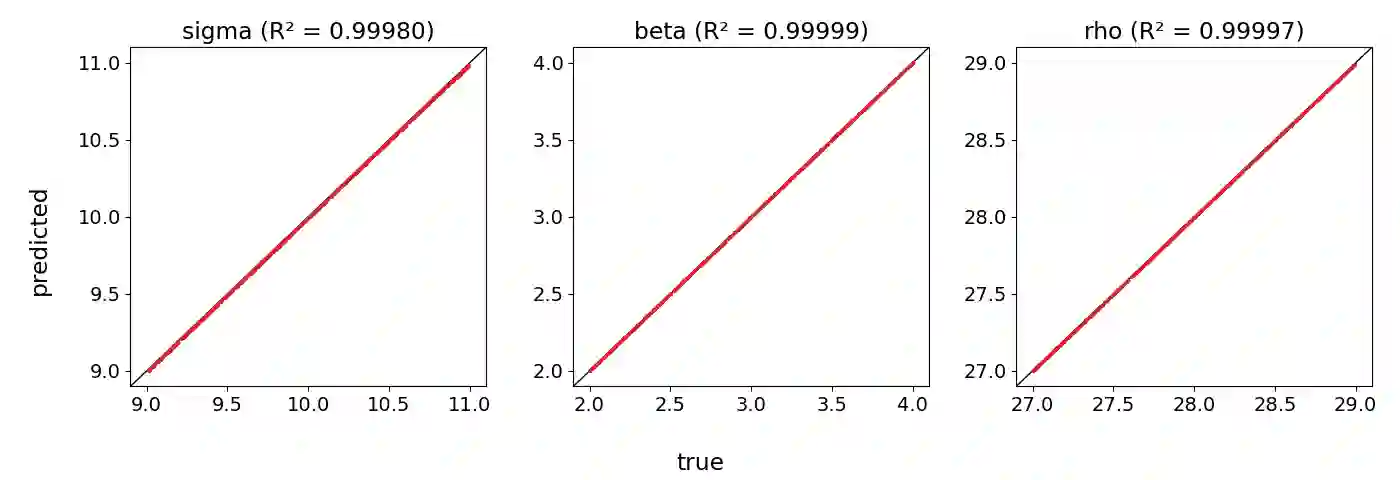
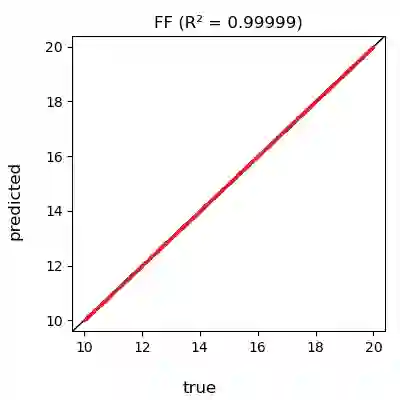
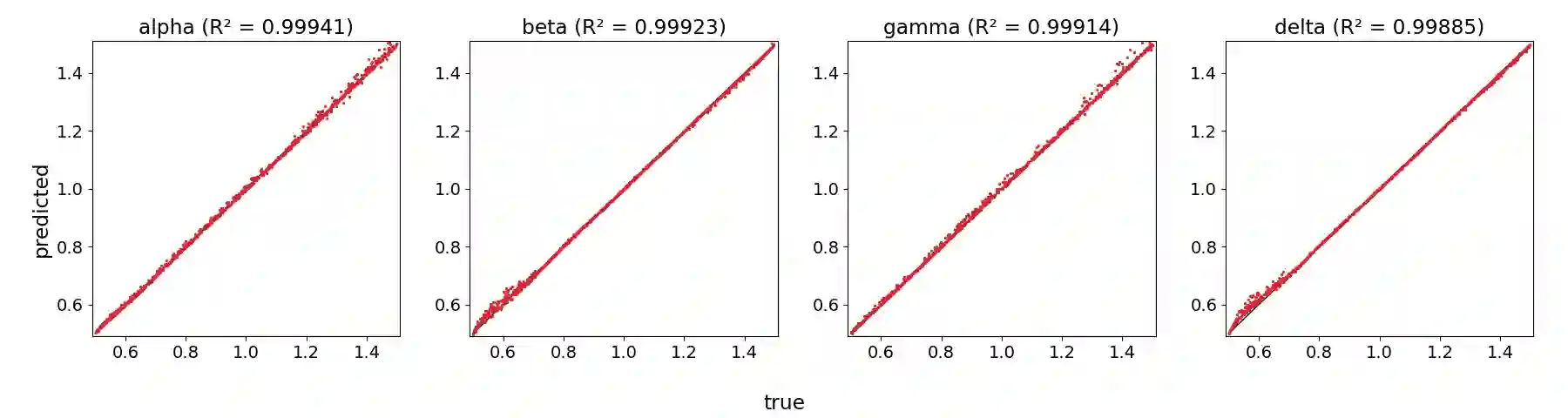
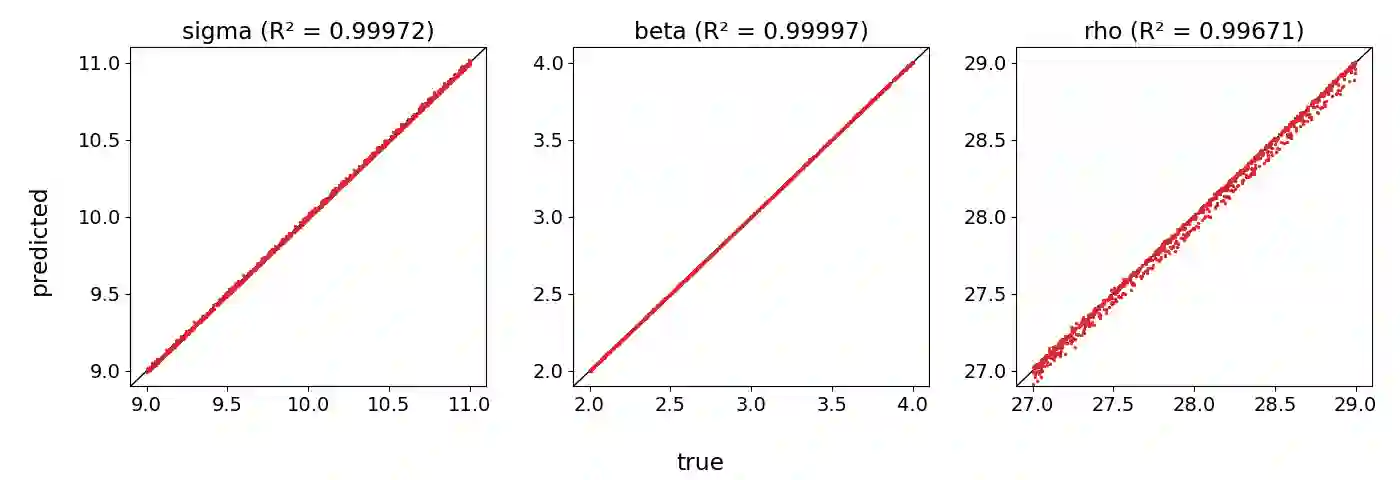
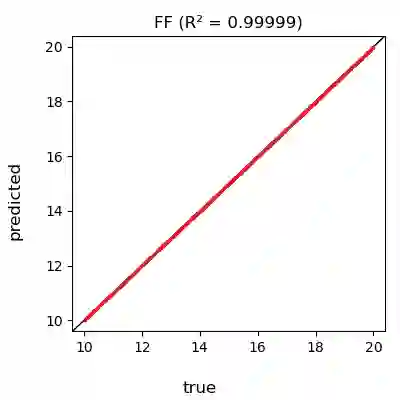
We provide a method to identify system parameters of dynamical systems, called ID-ODE -- Inference by Differentiation and Observing Delay Embeddings. In this setting, we are given a dataset of trajectories from a dynamical system with system parameter labels. Our goal is to identify system parameters of new trajectories. The given trajectories may or may not encompass the full state of the system, and we may only observe a one-dimensional time series. In the latter case, we reconstruct the full state by using delay embeddings, and under sufficient conditions, Taken's Embedding Theorem assures us the reconstruction is diffeomorphic to the original. This allows our method to work on time series. Our method works by first learning the velocity operator (as given or reconstructed) with a neural network having both state and system parameters as variable inputs. Then on new trajectories we backpropagate prediction errors to the system parameter inputs giving us a gradient. We then use gradient descent to infer the correct system parameter. We demonstrate the efficacy of our approach on many numerical examples: the Lorenz system, Lorenz96, Lotka-Volterra Predator-Prey, and the Compound Double Pendulum. We also apply our algorithm on a real-world dataset: propulsion of the Hall-effect Thruster (HET).
翻译:我们提供一种方法来确定动态系统的系统参数,称为 ID-ODE -- 通过差异和观察延迟嵌入来推断系统参数。 在这种环境下, 我们从一个带有系统参数标签的动态系统中获得一组关于轨迹的数据。 我们的目标是确定新轨迹的系统参数。 给定的轨迹可能包含系统的完整状态, 我们可能只观察一个一维的时间序列。 在后一种情况下, 我们通过延迟嵌入来重建整个状态, 并在充分的条件下, 嵌入的理论保证了我们重建的系统与原始系统不相容。 这样我们就可以在时间序列上工作的方法。 我们的方法是先用一个神经网络来学习速度操作器( 被授予或重建的), 其状态和系统参数作为变量输入的完整状态。 然后是新的轨迹, 我们把预测误差带给我们一个梯度的参数输入一个梯度。 然后我们用梯度来推断正确的系统参数参数参数参数参数。 我们用梯度来显示我们的方法在时间序列上的工作效率。 我们用许多数字例子来显示我们的方法: Rodl- Chil- hall 系统: Wereblexal- holdstal