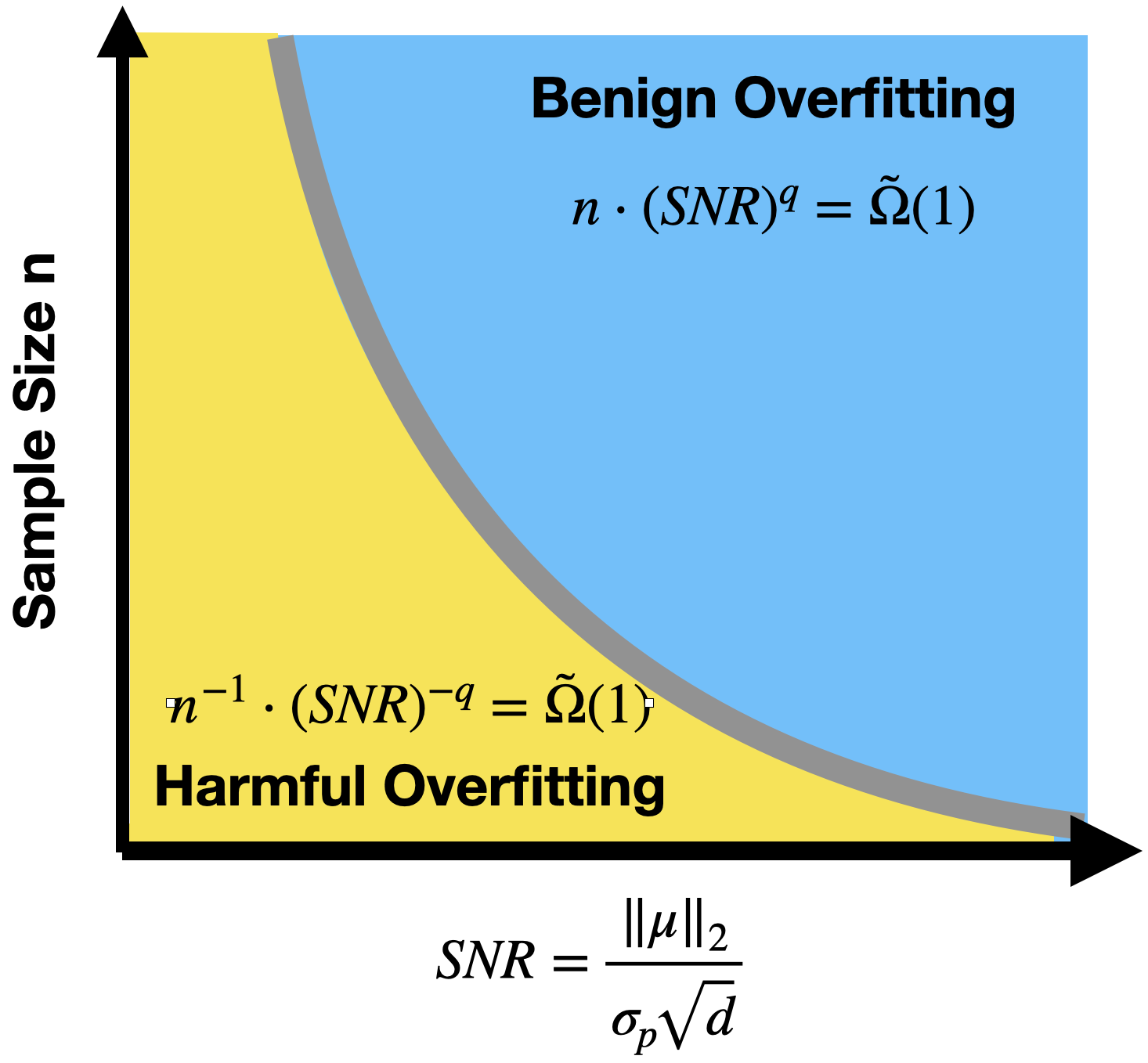
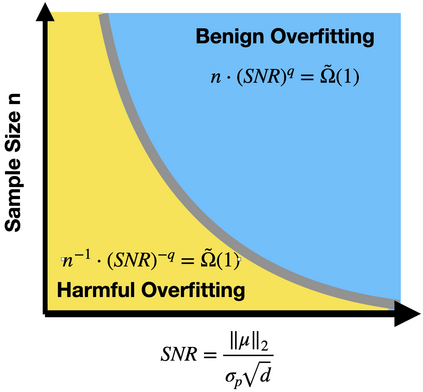
Modern neural networks often have great expressive power and can be trained to overfit the training data, while still achieving a good test performance. This phenomenon is referred to as "benign overfitting". Recently, there emerges a line of works studying "benign overfitting" from the theoretical perspective. However, they are limited to linear models or kernel/random feature models, and there is still a lack of theoretical understanding about when and how benign overfitting occurs in neural networks. In this paper, we study the benign overfitting phenomenon in training a two-layer convolutional neural network (CNN). We show that when the signal-to-noise ratio satisfies a certain condition, a two-layer CNN trained by gradient descent can achieve arbitrarily small training and test loss. On the other hand, when this condition does not hold, overfitting becomes harmful and the obtained CNN can only achieve a constant level test loss. These together demonstrate a sharp phase transition between benign overfitting and harmful overfitting, driven by the signal-to-noise ratio. To the best of our knowledge, this is the first work that precisely characterizes the conditions under which benign overfitting can occur in training convolutional neural networks.
翻译:现代神经网络通常具有巨大的表达力,并且可以接受培训,以过度配置培训数据,同时仍能取得良好的测试性能。这一现象被称为“隐性过度装饰 ” 。 最近,出现了从理论角度研究“ 隐性过度装饰” 特征模型的一连串工作。 但是,它们局限于线性模型或内核/内核/内核特质模型,对于神经网络何时和如何发生良性过度装饰仍然缺乏理论理解。 在本文中,我们在培训两层革命性神经网络(CNN)时研究适中过度装现象。 我们发现,当信号-噪音比率达到一定条件时,由梯度下降所训练的两层CNN可以实现任意的小型培训和测试损失。 另一方面,如果这种条件不能维持下去,过度装饰就会变得有害,获得的CNNC只能实现持续水平测试性损失。 这些共同表明,在良性过度装饰和有害性过度配配配配制之间,在信号-噪音比率驱动下发生了一个尖锐的阶段的转变。我们最了解的是,这是在培训中准确界定良性超度网络的条件的首项工作。