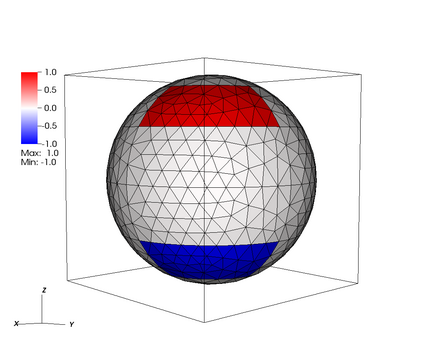
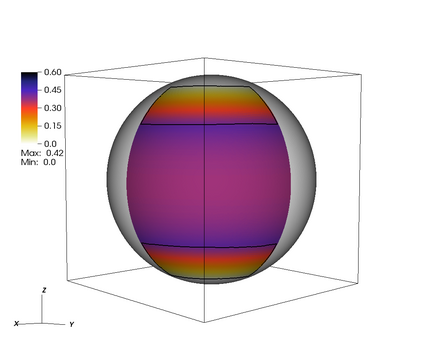
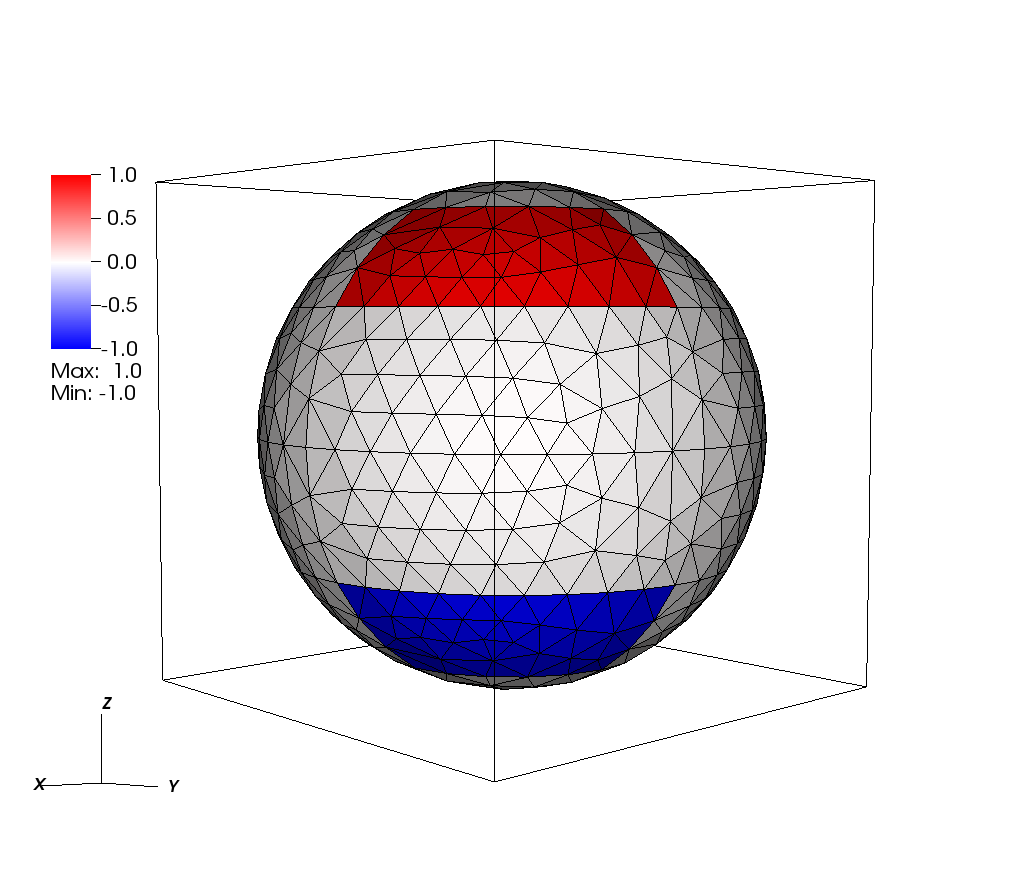
In this article we study the numerical solution of the $L^1$-Optimal Transport Problem on 2D surfaces embedded in $R^3$, via the DMK formulation introduced in [FaccaCardinPutti:2018]. We extend from the Euclidean into the Riemannian setting the DMK model and conjecture the equivalence with the solution Monge-Kantorovich equations, a PDE-based formulation of the $L^1$-Optimal Transport Problem. We generalize the numerical method proposed in [FaccaCardinPutti:2018,FaccaDaneriCardinPutti:2020] to 2D surfaces embedded in $\REAL^3$ using the Surface Finite Element Model approach to approximate the Laplace-Beltrami equation arising from the model. We test the accuracy and efficiency of the proposed numerical scheme, comparing our approximate solution with respect to an exact solution on a 2D sphere. The results show that the numerical scheme is efficient, robust, and more accurate with respect to other numerical schemes presented in the literature for the solution of ls$L^1$-Optimal Transport Problem on 2D surfaces.
翻译:在本篇文章中,我们研究了2D表面的1美元-最佳运输问题的数字解决办法,它嵌入了3美元,在[FaccaCardinPutti:2018]中引入了DMK配方。我们把Euclidean扩大到里曼尼安设置了DMK模型,并推测了与Monge-Kantorovich方程式的等值,Monge-Kantorovich方程式是以PDE为基础的一种配方,即1美元-最佳运输问题的精确解决办法。我们将[FaccacardinPutti:2018,FaccaDaneriCardinPutti:20]中提议的数值方法推广到2D表面表面的2D表,在使用地表固定要素模型方法确定为$\REAL3美元,以近似Laplace-Beltrami方程式。我们测试了拟议的数字办法的准确性和效率,将我们的近似解决办法与2D域的精确解决办法进行比较。结果显示,数字办法与SL1-O1-Mirmaimal Progisal Ex 问题的文献中的其他数字方案是高效、稳和准确的。