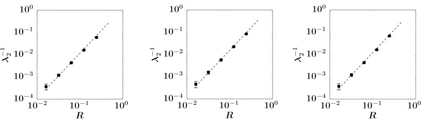
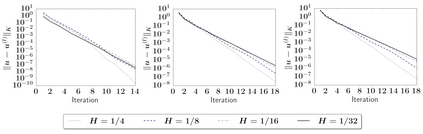
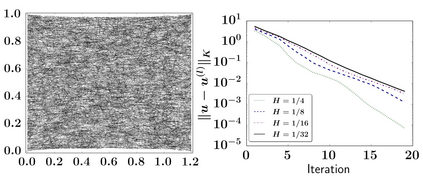
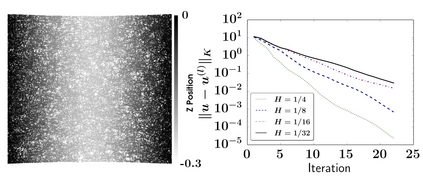
We present and analyze a preconditioned conjugate gradient method (PCG) for solving spatial network problems. Primarily, we consider diffusion and structural mechanics simulations for fiber based materials, but the methodology can be applied to a wide range of models, fulfilling a set of abstract assumptions. The proposed method builds on a classical subspace decomposition into a coarse subspace, realized as the restriction of a finite element space to the nodes of the spatial network, and localized subspaces with support on mesh stars. The main contribution of this work is the convergence analysis of the proposed method. The analysis translates results from finite element theory, including interpolation bounds, to the spatial network setting. A convergence rate of the PCG algorithm, only depending on global bounds of the operator and homogeneity, connectivity and locality constants of the network, is established. The theoretical results are confirmed by several numerical experiments.
翻译:我们提出并分析一种解决空间网络问题的先决条件的同流梯度方法(PCG) 。 我们首先考虑纤维材料的传播和结构机械模拟,但该方法可以适用于广泛的模型,实现一套抽象的假设。拟议方法建立在古典的子空间分解成粗糙的子空间上,这是限制空间网络节点的有限元素空间和对网星支持的局部子空间所实现的。这项工作的主要贡献是对拟议方法的趋同分析。分析将有限元素理论(包括内插界限)转化为空间网络设置的结果。 PCG算法的趋同率仅取决于操作者的全球界限和网络的同质性、连通性和地点常数。 理论结果得到了数项实验的证实。