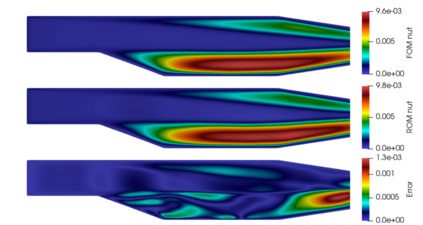
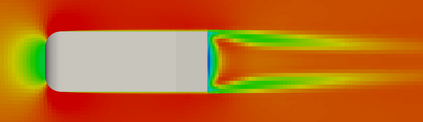
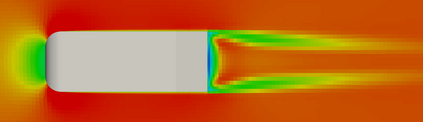
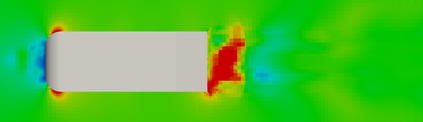
Geometrically parametrized Partial Differential Equations are nowadays widely used in many different fields as, for example, shape optimization processes or patient specific surgery studies. The focus of this work is on some advances for this topic, capable of increasing the accuracy with respect to previous approaches while relying on a high cost-benefit ratio performance. The main scope of this paper is the introduction of a new technique mixing up a classical Galerkin-projection approach together with a data-driven method to obtain a versatile and accurate algorithm for the resolution of geometrically parametrized incompressible turbulent Navier-Stokes problems. The effectiveness of this procedure is demonstrated on two different test cases: a classical academic back step problem and a shape deformation Ahmed body application. The results show into details the properties of the architecture we developed while exposing possible future perspectives for this work.
翻译:目前,在许多不同领域广泛使用几何对称偏差部分等分法,例如,形状优化过程或针对病人的外科研究。这项工作的重点是这一专题的一些进展,能够提高以往方法的准确性,同时依靠高成本效益比的性能。本文件的主要范围是采用一种新的技术,将古典的加勒金预测法与数据驱动法结合起来,以获得一种多功能和准确的算法,解决几何对称对称不可压缩的动荡纳维埃-斯托克斯问题。这一程序的有效性体现在两个不同的试验案例上:典型的学术后步问题和艾哈迈德身体形状变形应用。结果详细显示了我们所开发的结构的特性,同时暴露了这项工作的未来可能前景。