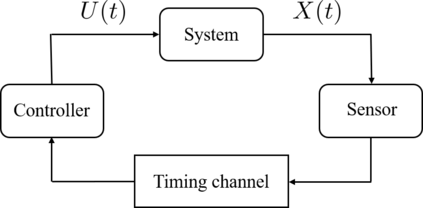
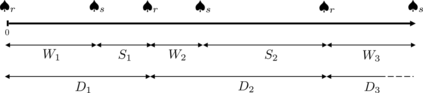
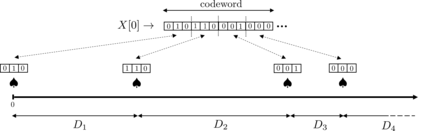
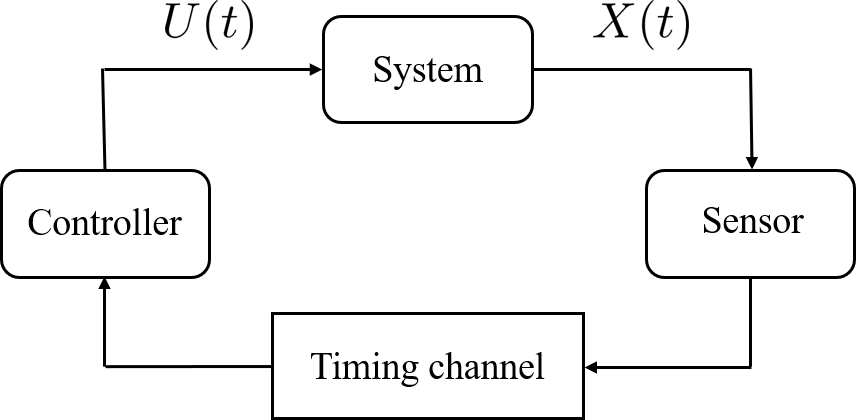
We consider the problem of stabilizing an undisturbed, scalar, linear system over a "timing" channel, namely a channel where information is communicated through the timestamps of the transmitted symbols. Each symbol transmitted from a sensor to a controller in a closed-loop system is received subject to some to random delay. The sensor can encode messages in the waiting times between successive transmissions and the controller must decode them from the inter-reception times of successive symbols. This set-up is analogous to a telephone system where a transmitter signals a phone call to a receiver through a "ring" and, after the random delay required to establish the connection; the receiver is aware of the "ring" being received. Since there is no data payload exchange between the sensor and the controller, this set-up provides an abstraction for performing event-triggering control with zero-payload rate. We show the following requirement for stabilization: for the state of the system to converge to zero in probability, the timing capacity of the channel should be, essentially, at least as large as the entropy rate of the system. Conversely, in the case the symbol delays are exponentially distributed, we show an "almost" tight sufficient condition using a coding strategy that refines the estimate of the decoded message every time a new symbol is received. Our results generalize previous zero-payload event-triggering control strategies, revealing a fundamental limit in using timing information for stabilization, independent of any transmission strategy.
翻译:我们考虑稳定一个“ 触发” 频道上未扰动、 斜线、 线性系统的问题, 即一个通过传输符号的时间戳传递信息的频道。 接收从传感器传送到闭环系统中控制器的每个符号时会受到一些随机的延迟。 传感器可以在连续传输和控制器之间等待时间将信件编码成连续符号的跨接收时间。 这个设置类似于一个电话系统, 即发送器通过“ 环” 和在建立连接所需的随机延迟后向接收器发出电话信号的频道; 接收器知道接收到的“ 环” 。 由于传感器和控制器之间没有数据有效交换, 接收到的每个符号, 这个设置提供了一个抽象的设置, 用于执行以零支付率进行事件触发控制。 我们显示以下的稳定要求: 系统状态要接近于概率为零, 频道的定时能力应该至少是“ 系统最大幅度的连接率 ; 最短的传输速度, 反之, 使用最接近的标志性时间轴战略, 使用最精确的精确的精确时间间隔战略, 显示我们所收到的基本信号的精确的精确的顺序控制结果 。 我们显示一个总的精确的精确的精确的精确的路径 。 将显示, 将显示, 发送的精确的精确的精确的策略将显示结果 。