On attainability of Kendall's tau matrices and concordance signatures

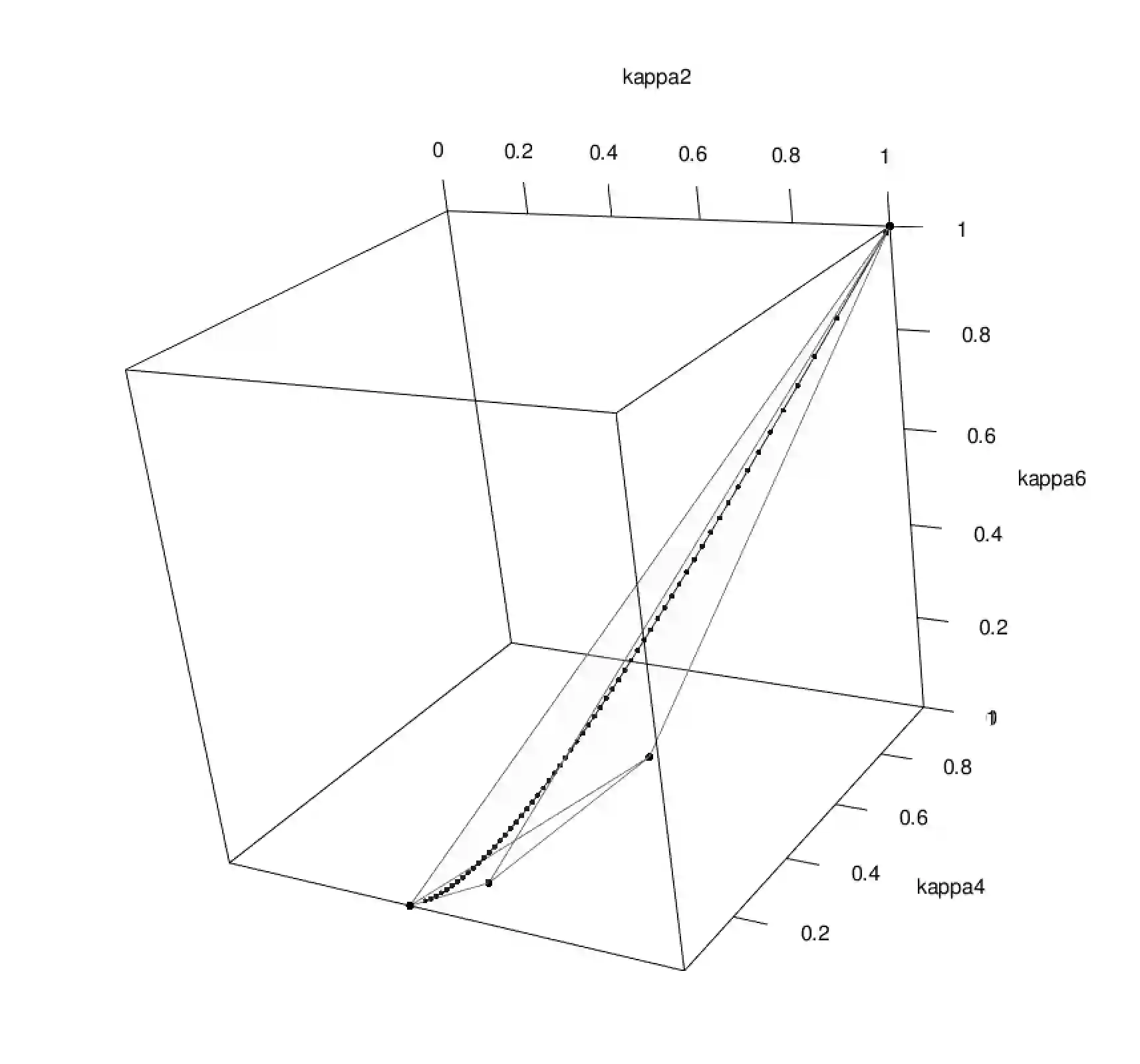
Methods are developed for checking and completing systems of bivariate and multivariate Kendall's tau concordance measures in applications where only partial information about dependencies between variables is available. The concept of a concordance signature of a multivariate continuous distribution is introduced; this is the vector of concordance probabilities for margins of all orders. It is shown that every attainable concordance signature is equal to the concordance signature of a unique mixture of the extremal copulas, that is the copulas with extremal correlation matrices consisting exclusively of 1's and -1's. A method of estimating an attainable concordance signature from data is derived and shown to correspond to using standard estimates of Kendall's tau in the absence of ties. The set of attainable Kendall rank correlation matrices of multivariate continuous distributions is proved to be identical to the set of convex combinations of extremal correlation matrices, a set known as the cut polytope. A methodology for testing the attainability of concordance signatures using linear optimization and convex analysis is provided. The elliptical copulas are shown to yield a strict subset of the attainable concordance signatures as well as a strict subset of the attainable Kendall rank correlation matrices; the Student t copula is seen to converge, as the degrees of freedom tend to zero, to a mixture of extremal copulas sharing its concordance signature with all elliptical distributions that have the same correlation matrix. A characterization of the attainable signatures of equiconcordant copulas is given.