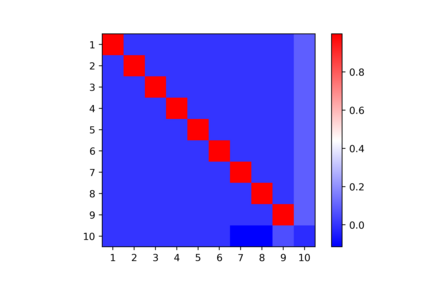
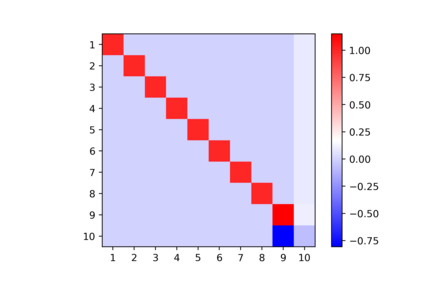
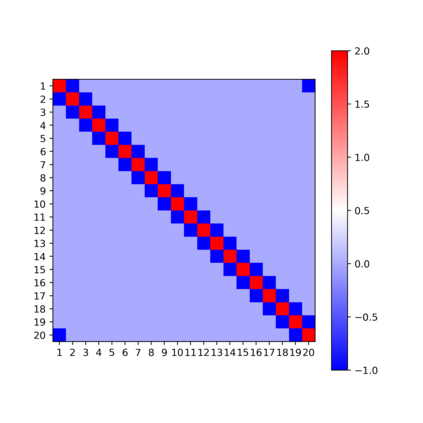
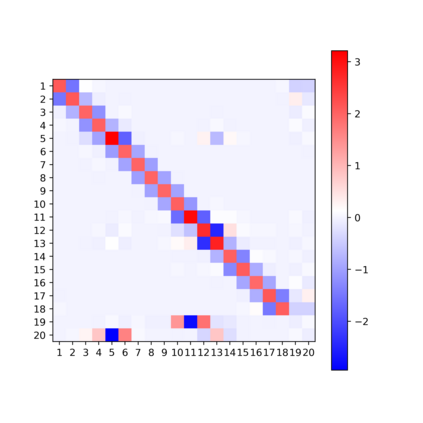
In this note, we consider the optimization problem associated with computing the rank decomposition of a symmetric tensor. We show that, in a well-defined sense, minima in this highly nonconvex optimization problem break the symmetry of the target tensor -- but not too much. This phenomenon of symmetry breaking applies to various choices of tensor norms, and makes it possible to study the optimization landscape using a set of recently-developed symmetry-based analytical tools. The fact that the objective function under consideration is a multivariate polynomial allows us to apply symbolic methods from computational algebra to obtain more refined information on the symmetry breaking phenomenon.
翻译:在本说明中,我们考虑了与计算对称振标的分解等级相关的优化问题。我们表明,在定义明确的意义上,这个高度非电流优化问题的微小打破了目标振标的对称性,但并不太多。这种对称性断裂现象适用于对振标的各种选择,并使得有可能使用最近开发的一套对称分析工具来研究优化景观。事实上,所考虑的客观功能是多变量的多元数学,这使我们能够从计算代数中应用符号方法来获取关于对称断裂现象的更精细的信息。