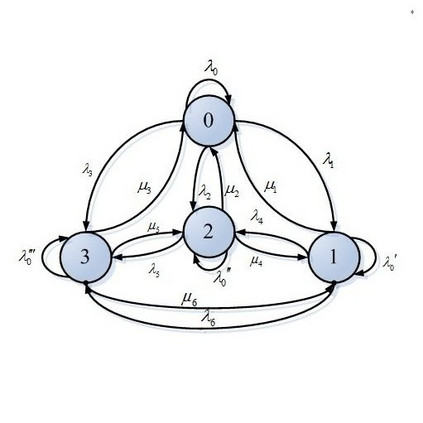
This paper considers estimating the parameters in a regime-switching stochastic differential equation(SDE) driven by Normal Inverse Gaussian(NIG) noise. The model under consideration incorporates a continuous-time finite state Markov chain to capture regime changes, enabling a more realistic representation of evolving market conditions or environmental factors. Although the continuous dynamics are typically observable, the hidden nature of the Markov chain introduces significant complexity, rendering standard likelihood-based methods less effective. To address these challenges, we propose an estimation algorithm designed for discrete, high-frequency observations, even when the Markov chain is not directly observed. Our approach integrates the Expectation-Maximization (EM) algorithm, which iteratively refines parameter estimates in the presence of latent variables, with a quasi-likelihood method adapted to NIG noise. Notably, this method can simultaneously estimate parameters within both the SDE coefficients and the driving noise. Simulation results are provided to evaluate the performance of the algorithm. These experiments demonstrate that the proposed method provides reasonable estimation under challenging conditions.
翻译:暂无翻译