Tree boosting for learning probability measures

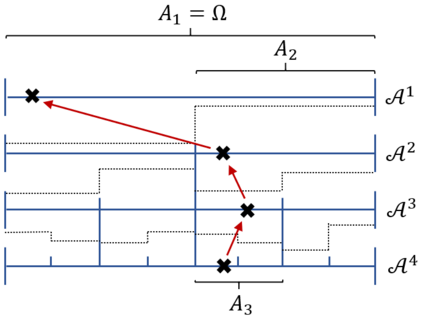
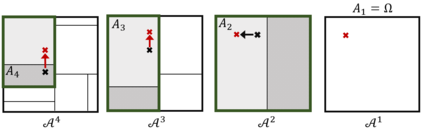
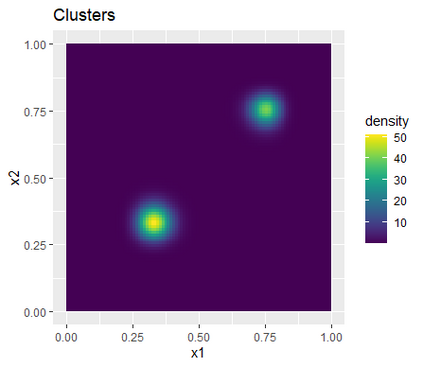
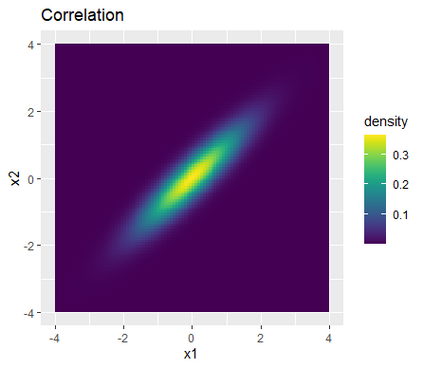
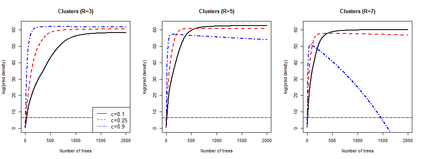
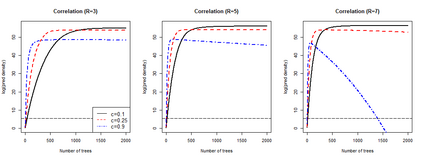
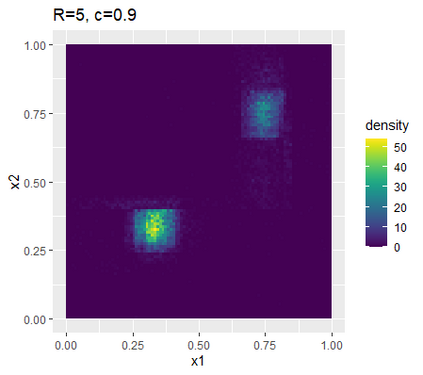
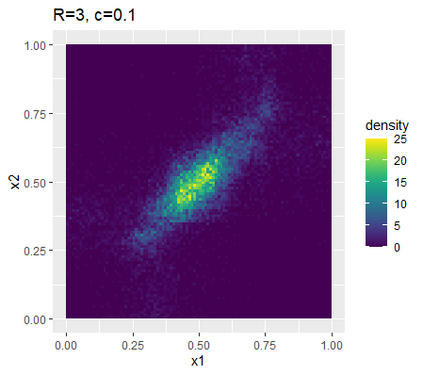
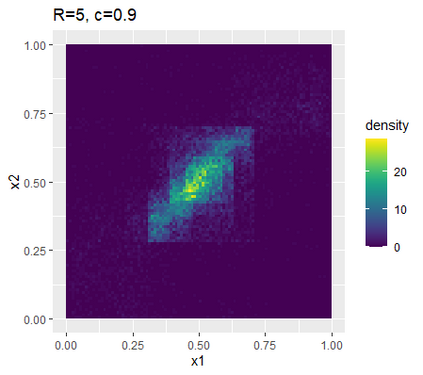
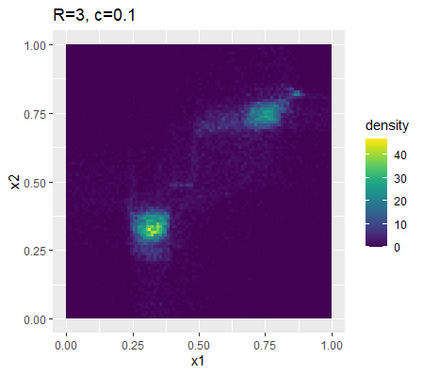
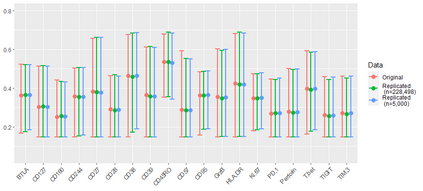
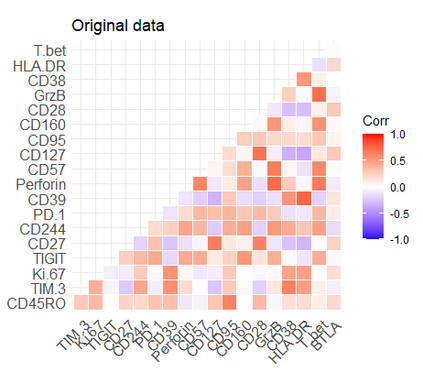
Learning probability measures based on an i.i.d. sample is a fundamental inference task, but is challenging when the sample space is high-dimensional. Inspired by the success of tree boosting in high-dimensional classification and regression, we propose a tree boosting method for learning high-dimensional probability distributions. We formulate concepts of "addition'' and "residuals'' on probability distributions in terms of compositions of a new, more general notion of multivariate cumulative distribution functions (CDFs) than classical CDFs. This then gives rise to a simple boosting algorithm based on forward-stagewise (FS) fitting of an additive ensemble of measures. The output of the FS algorithm allows analytic computation of the probability density function for the fitted distribution. It also provides an exact simulator for drawing independent Monte Carlo samples from the fitted measure. Typical considerations in applying boosting -- namely choosing the number of trees, setting the appropriate level of shrinkage/regularization in the weak learner, and the evaluation of variable importance -- can be accomplished in an analogous fashion to traditional boosting in supervised learning. Numerical experiments confirm that boosting can substantially improve the fit to multivariate distributions compared to the state-of-the-art single-tree learner and is computationally efficient. We illustrate through an application to a data set from mass cytometry how the simulator can be used to investigate various aspects of the underlying distribution.