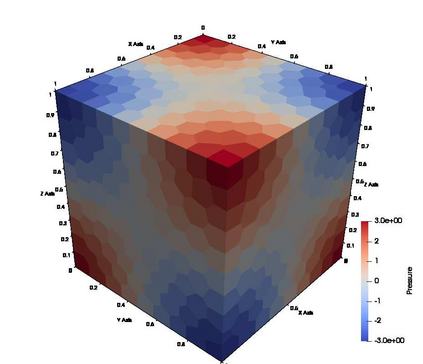
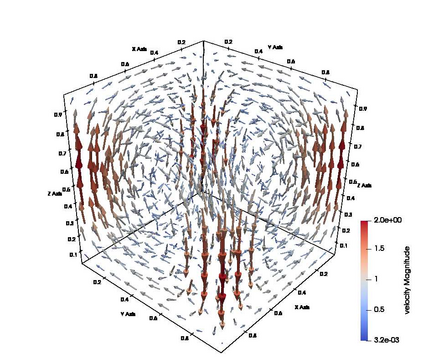
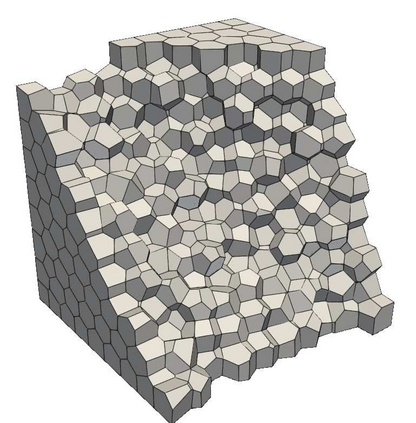
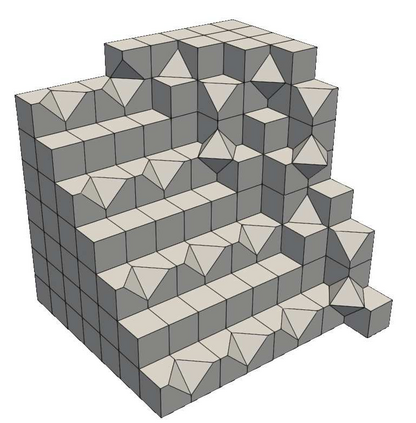
The Virtual Element Method (VEM) is a novel family of numerical methods for approximating partial differential equations on very general polygonal or polyhedral computational grids. This work aims to propose a Balancing Domain Decomposition by Constraints (BDDC) preconditioner that allows using the conjugate gradient method to compute the solution of the saddle-point linear systems arising from the VEM discretization of the three-dimensional Stokes equations. We prove the scalability and quasi-optimality of the algorithm and confirm the theoretical findings with parallel computations. Numerical results with adaptively generated coarse spaces confirm the method's robustness in the presence of large jumps in the viscosity and with high-order VEM discretizations.
翻译:虚拟元素法(VEM)是一系列新型数值方法,可在非常通用的多边形或多面体计算网格上逼近偏微分方程。本文旨在提出一个平衡域分解约束(BDDC)预处理器,使得可以使用共轭梯度方法计算三维Stokes方程的VEM离散化得到的鞍点线性系统的解。我们证明了该算法的可扩展性和准最优性,并用并行计算证实了理论的发现。 自适应生成粗略空间的数值结果证实了该方法在粘度大幅跃变和高阶VEM离散化的情况下的鲁棒性。