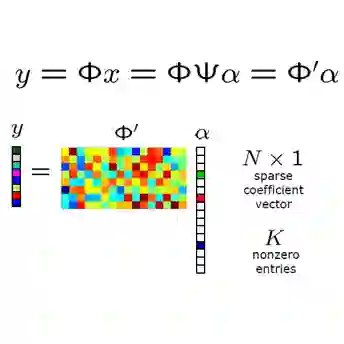
Compressed sensing for inverse problems and the sample complexity of the sparse Radon transform

Compressed sensing allows for the recovery of sparse signals from few measurements, whose number is proportional to the sparsity of the unknown signal, up to logarithmic factors. The classical theory typically considers either random linear measurements or subsampled isometries and has found many applications, including accelerated magnetic resonance imaging, which is modeled by the subsampled Fourier transform. In this work, we develop a general theory of infinite-dimensional compressed sensing for abstract inverse problems, possibly ill-posed, involving an arbitrary forward operator. This is achieved by considering a generalized restricted isometry property, and a quasi-diagonalization property of the forward map. As a notable application, for the first time, we obtain rigorous recovery estimates for the sparse Radon transform (i.e., with a finite number of angles $\theta_1,\dots,\theta_m$), which models computed tomography. In the case when the unknown signal is $s$-sparse with respect to an orthonormal basis of compactly supported wavelets, we prove exact recovery under the condition \[ m\gtrsim s, \] up to logarithmic factors.