Optimal Supersaturated Designs for Lasso Sign Recovery

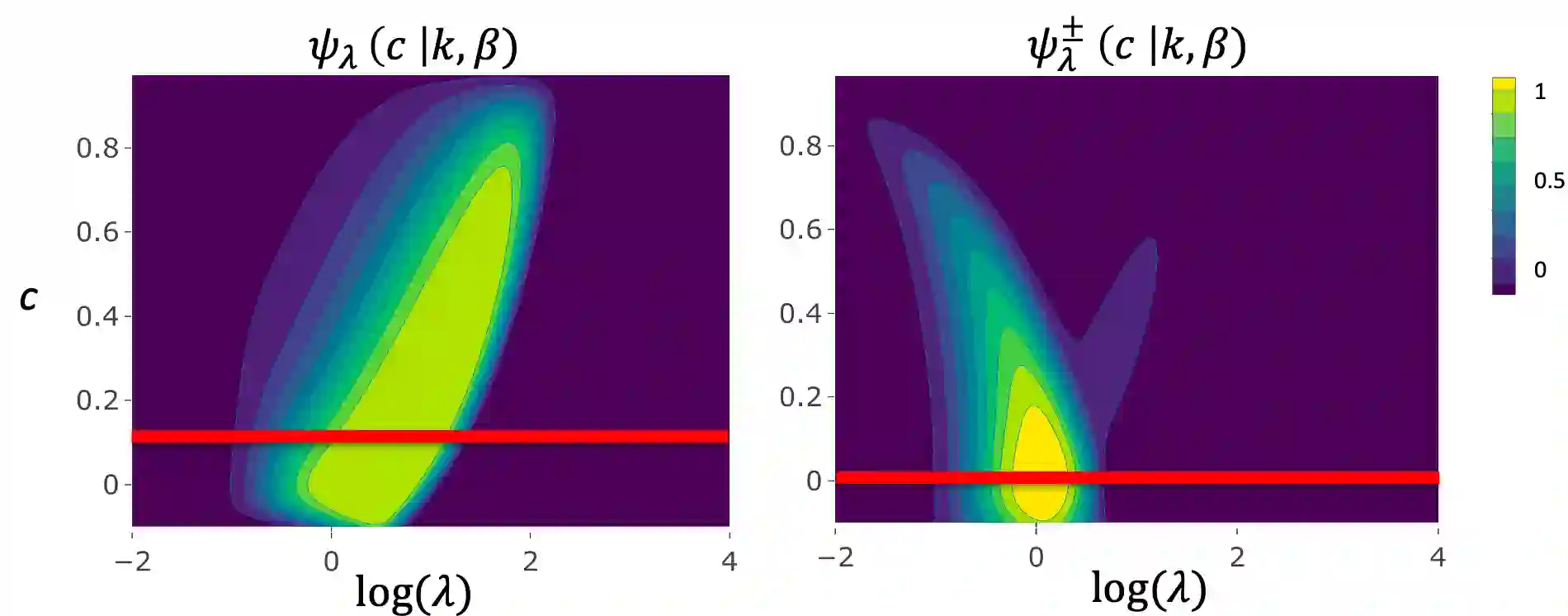
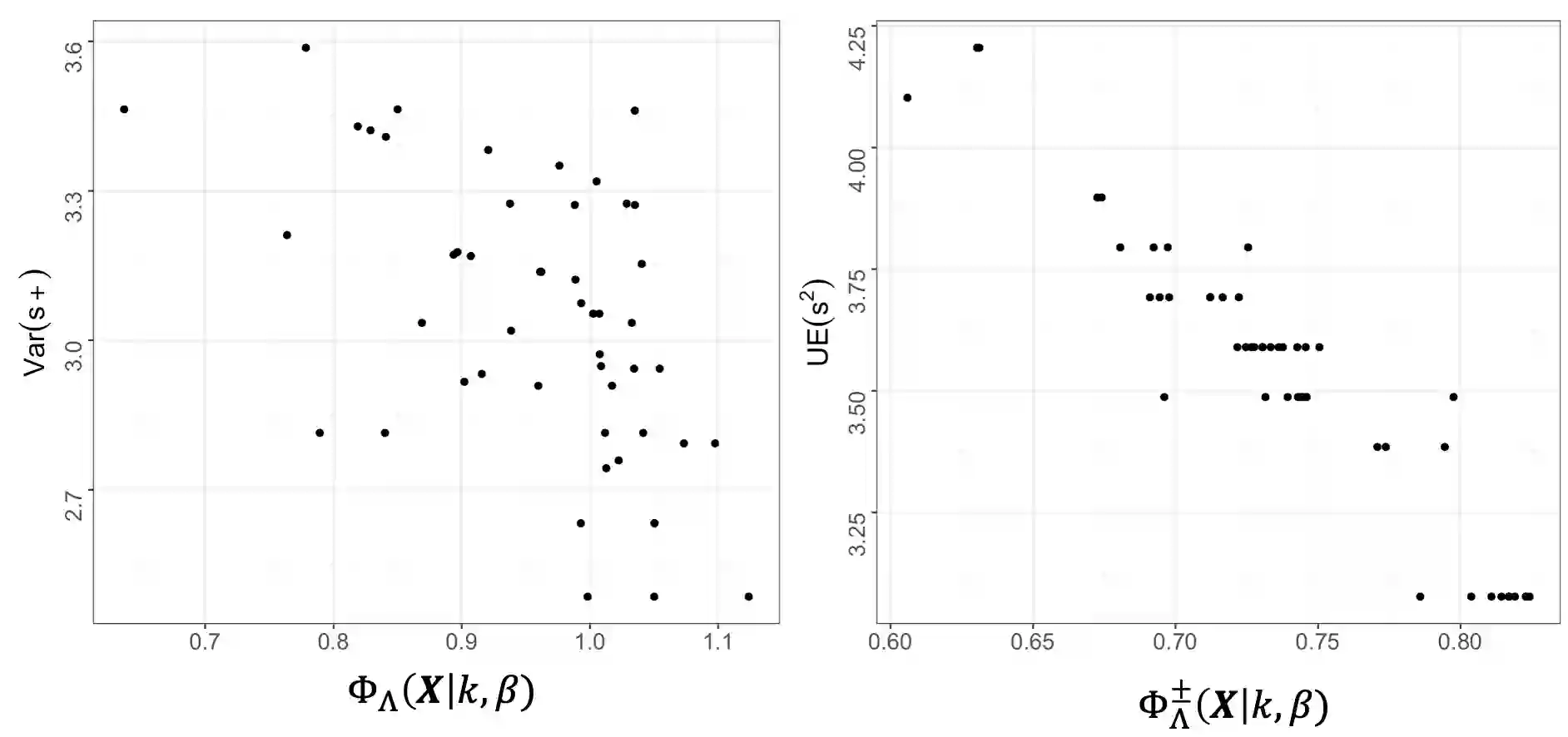
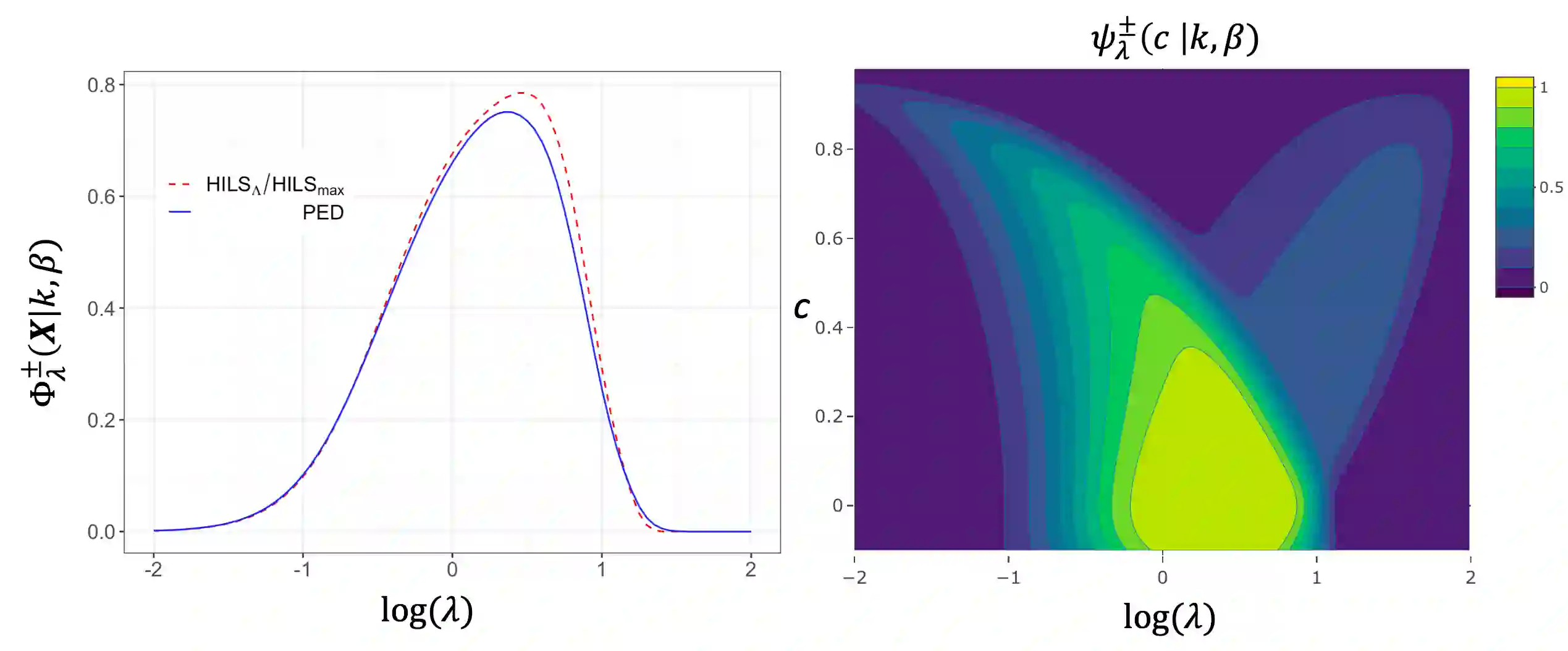
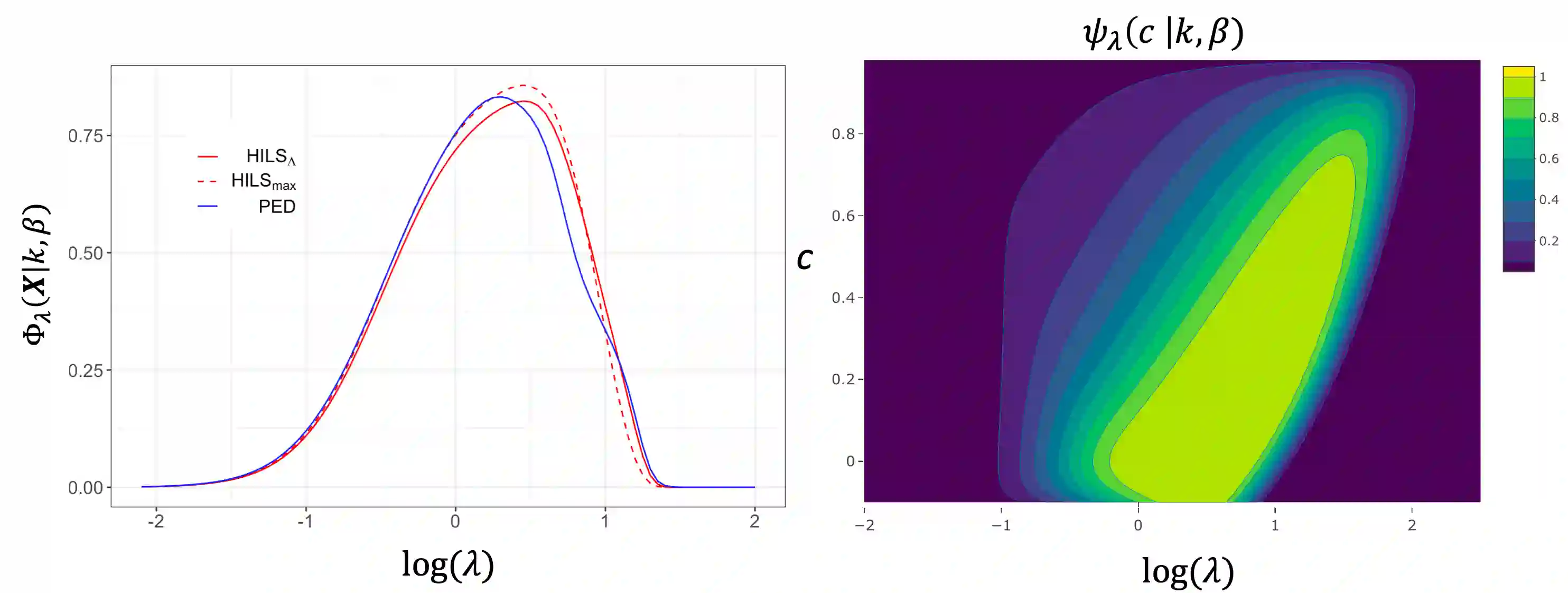
Supersaturated designs, in which the number of factors exceeds the number of runs, are often constructed under a heuristic criterion that measures a design's proximity to an unattainable orthogonal design. Such a criterion does not directly measure a design's quality in terms of screening. To address this disconnect, we develop optimality criteria to maximize the lasso's sign recovery probability. The criteria have varying amounts of prior knowledge about the model's parameters. We show that an orthogonal design is an ideal structure when the signs of the active factors are unknown. When the signs are assumed known, we show that a design whose columns exhibit small, positive correlations are ideal. Such designs are sought after by the Var(s+)-criterion. These conclusions are based on a continuous optimization framework, which rigorously justifies the use of established heuristic criteria. From this justification, we propose a computationally-efficient design search algorithm that filters through optimal designs under different heuristic criteria to select the one that maximizes the sign recovery probability under the lasso.