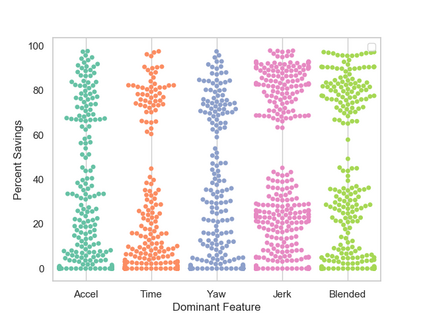
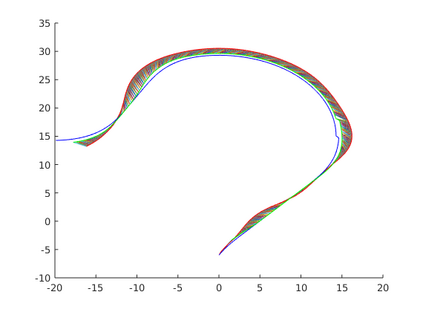
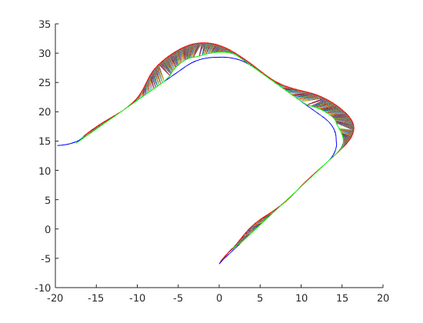
Trajectory planning is commonly used as part of a local planner in autonomous driving. This paper considers the problem of planning a continuous-curvature-rate trajectory between fixed start and goal states that minimizes a tunable trade-off between passenger comfort and travel time. The problem is an instance of infinite dimensional optimization over two continuous functions: a path, and a velocity profile. We propose a simplification of this problem that facilitates the discretization of both functions. This paper also proposes a method to quickly generate minimal-length paths between start and goal states based on a single tuning parameter: the second derivative of curvature. Furthermore, we discretize the set of velocity profiles along a given path into a selection of acceleration way-points along the path. Gradient-descent is then employed to minimize cost over feasible choices of the second derivative of curvature, and acceleration way-points, resulting in a method that repeatedly solves the path and velocity profiles in an iterative fashion. Numerical examples are provided to illustrate the benefits of the proposed methods.
翻译:轨迹规划通常作为本地自动驾驶规划师的一部分使用。 本文考虑了规划固定起始点与目标之间连续曲率轨迹的问题, 指出在乘客舒适度和旅行时间之间最大限度地减少可缓冲的平衡。 问题是两个连续函数的无限维度优化: 路径和速度剖面。 我们建议简化这个问题, 便利两种函数的分离。 本文件还提出一种方法, 以单一调试参数( 曲线的第二个衍生物) 为基础, 在起始点和目标点之间快速生成最短长度的路径。 此外, 我们将特定路径上的速度剖析图集分解为一条选择路径的加速路点。 然后, 梯度- 白度用于在二次曲线衍生物和加速路点的可行选择上将成本最小化, 导致反复解决路径和速度剖面的方法。 提供了数字示例, 以说明拟议方法的效益 。