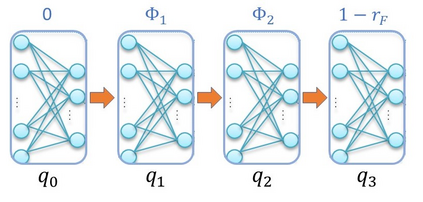
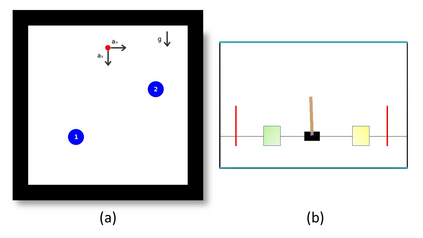
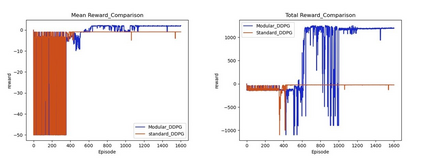
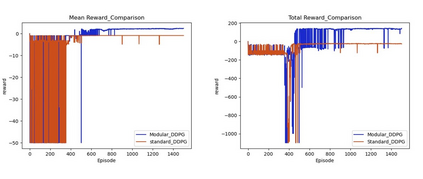
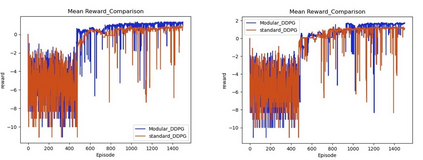
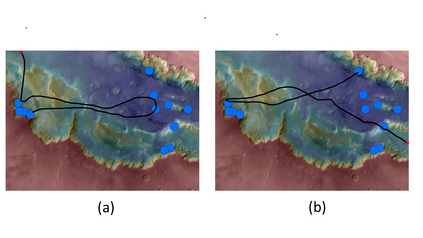
This paper investigates the motion planning of autonomous dynamical systems modeled by Markov decision processes (MDP) with unknown transition probabilities over continuous state and action spaces. Linear temporal logic (LTL) is used to specify high-level tasks over infinite horizon, which can be converted into a limit deterministic generalized B\"uchi automaton (LDGBA) with several accepting sets. The novelty is to design an embedded product MDP (EP-MDP) between the LDGBA and the MDP by incorporating a synchronous tracking-frontier function to record unvisited accepting sets of the automaton, and to facilitate the satisfaction of the accepting conditions. The proposed LDGBA-based reward shaping and discounting schemes for the model-free reinforcement learning (RL) only depend on the EP-MDP states and can overcome the issues of sparse rewards. Rigorous analysis shows that any RL method that optimizes the expected discounted return is guaranteed to find an optimal policy whose traces maximize the satisfaction probability. A modular deep deterministic policy gradient (DDPG) is then developed to generate such policies over continuous state and action spaces. The performance of our framework is evaluated via an array of OpenAI gym environments.
翻译:本文调查了由Markov决定程序(MDP)建模的自主动态系统动态规划,该动态动态系统在连续状态和动作空间上具有未知的过渡概率。线性时间逻辑(LTL)用于指定无限地平线的高级任务,这些任务可以转换成一个有限的确定性通用B\"uchi automaton(LDGBA),具有几组接受性。新颖之处在于在LDGBA和MDP之间设计一个嵌入的产品MDP(EP-MDP)(EP-MDP),采用同步跟踪-前沿功能,记录未监视的接受自动马顿数据集,并促进接受条件的满足性。拟议的基于LDGBA的无模式强化学习(RL)奖励制成和折扣计划仅取决于EP-MDP(RL)的状态,并能够克服微量回报问题。严格分析表明,任何优化预期的贴现回报的RL方法都保证找到最佳政策,其痕迹最大化。随后将开发一个模块化的深度确定性政策梯度梯度梯度梯度(DPG),以便形成一个连续的阵列环境。
相关内容
Source: Apple - iOS 8