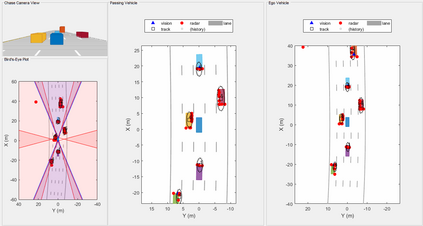
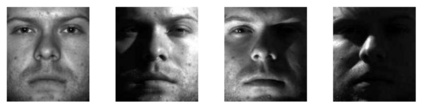
Many problems in signal processing and machine learning can be formalized as weak submodular optimization tasks. For such problems, a simple greedy algorithm (\textsc{Greedy}) is guaranteed to find a solution achieving the objective with a value no worse than $1-e^{-1/c}$ of the optimal, where $c$ is the multiplicative weak-submodularity constant. Due to the high cost of querying large-scale systems, the complexity of \textsc{Greedy} becomes prohibitive in contemporary applications. In this work, we study the tradeoff between performance and complexity when one resorts to random sampling strategies to reduce the query complexity of \textsc{Greedy}. Specifically, we quantify the effect of uniform sampling strategies on \textsc{Greedy}'s performance through two metrics: (i) probability of identifying an optimal subset, and (ii) suboptimality with respect to the optimal solution. The latter implies that uniform sampling strategies with a fixed sampling size achieve a non-trivial approximation factor; however, we show that with overwhelming probability, these methods fail to find the optimal subset. Our analysis shows that the failure of uniform sampling strategies with fixed sample size can be circumvented by successively increasing the size of the search space. Building upon this insight, we propose a simple progressive stochastic greedy algorithm and study its approximation guarantees. Moreover, we demonstrate effectiveness of the proposed method in dimensionality reduction applications and feature selection tasks for clustering and object tracking.
翻译:信号处理和机器学习方面的许多问题可以作为薄弱的子模块优化任务而正式化。 对于这些问题,我们保证,简单的贪婪算法(\ textsc{Greedy})能够找到一个解决方案来实现目标,其价值不低于1美元/e ⁇ - ⁇ -1/c}美元的最佳值,其中美元是多倍化的薄弱子模块常数。由于质疑大型系统的成本很高,因此在当代应用中,\ textsc{Greedy}的复杂性变得令人望而却步。在这项工作中,当我们采用随机抽样战略来降低\ textsc{Greedy}的查询复杂性时,我们研究性能和复杂性之间的权衡。具体地说,我们量化统一取样战略对以下两个衡量标准的效果:(一) 确定一个最佳子集的可能性,以及(二) 与最佳解决方案相比的亚优性。后者意味着,具有固定取样规模的统一抽样战略可以达到一个非三端近端的近效因素;然而,我们用惊人的概率来量化统一采样战略的效果。 我们提议,在不断的精确的排序中,这些方法会显示我们以最差的排序的排序的递化的方法来显示,我们的递增的递缩的精确的精确的排序。