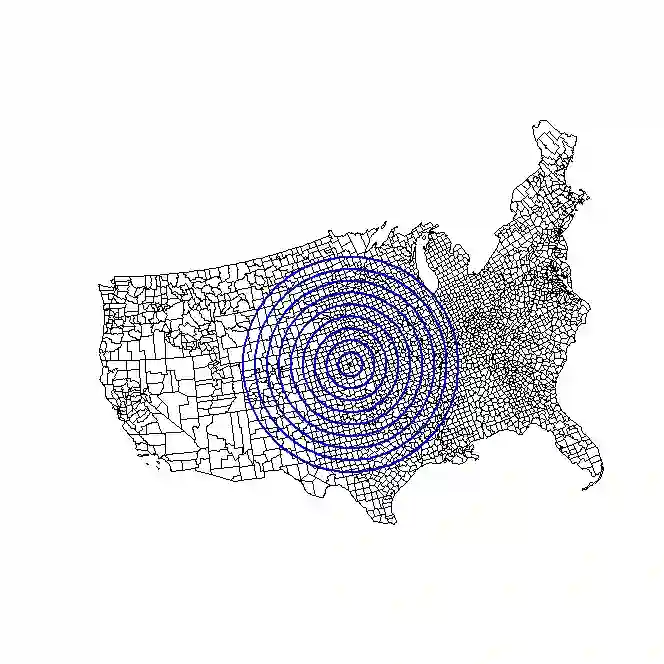
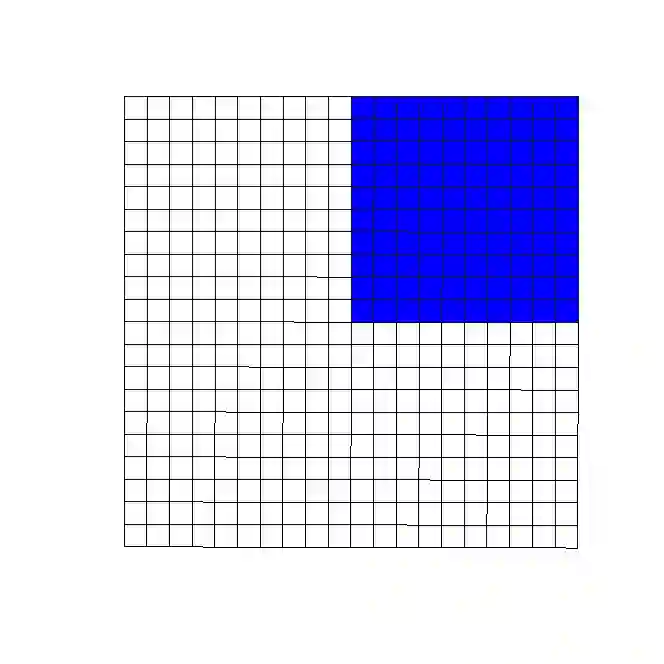
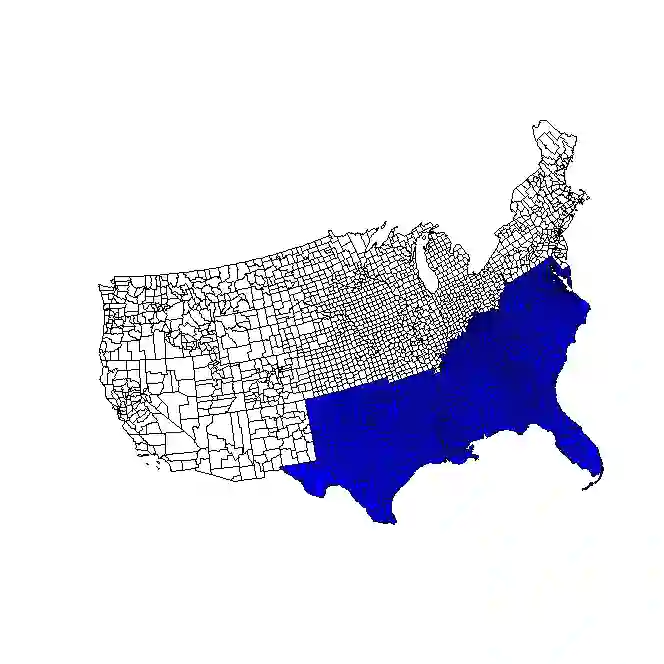
Spatial clustering detection has a variety of applications in diverse fields, including identifying infectious disease outbreaks, assessing land use patterns, pinpointing crime hotspots, and identifying clusters of neurons in brain imaging applications. While performing spatial clustering analysis on point process data is common, applications to areal data are frequently of interest. For example, researchers might wish to know if census tracts with a case of a rare medical condition or an outbreak of an infectious disease tend to cluster together spatially. Since few spatial clustering methods are designed for areal data, researchers often reduce the areal data to point process data (e.g., using the centroid of each areal unit) and apply methods designed for point process data, such as Ripley's K function or the average nearest neighbor method. However, since these methods were not designed for areal data, a number of issues can arise. For example, we show that they can result in loss of power and/or a significantly inflated type I error rate. To address these issues, we propose a generalization of Ripley's K function designed specifically to detect spatial clustering in areal data. We compare its performance to that of the traditional Ripley's K function, the average nearest neighbor method, and the spatial scan statistic with an extensive simulation study. We then evaluate the real world performance of the method by using it to detect spatial clustering in land parcels containing conservation easements and US counties with high pediatric overweight/obesity rates.
翻译:空间群集探测在不同领域有各种各样的应用,包括确定传染病爆发、评估土地使用模式、确定犯罪热点、确定大脑成像应用中的神经元群。在对点程数据进行空间群集分析是常见的,但对部分数据的应用经常引起兴趣。例如,研究人员可能希望知道,如果普查片段中存在罕见的医疗状况或传染病爆发的情况,那么,空间群集方法往往会集中在空间群集中。由于空间群集方法很少设计为部分数据,研究人员往往将数据减少到点处理数据(例如,使用每个单位的中间体),并应用为点处理数据设计的方法,如里普利的K函数或平均近邻方法。然而,由于这些方法不是为局部数据设计的,因此可能会出现一些问题。例如,我们表明,它们可能导致权力丧失和/或严重膨胀的I型误率。为了解决这些问题,我们建议对里普利的K函数进行概括,专门用来探测空间群集的数据(例如,使用每个单位的中间体),并应用为点进程数据设计的方法。我们用传统里普雷普利的功能来比较其业绩,而采用传统的空间群集速度,而用高的Smalimeximal Sty AS压方法来评估全球的地面群集,我们用空间群集法进行全球空间群集测测测测测的深度的地面的地面的地面的地面压法。