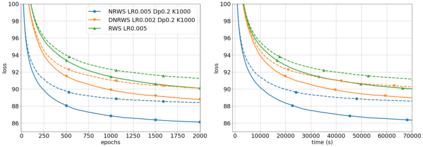
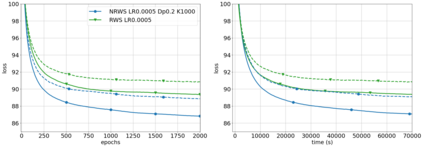
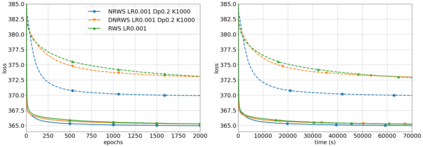
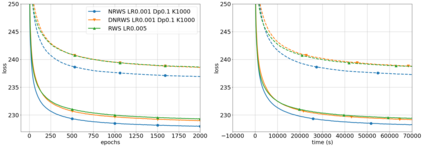
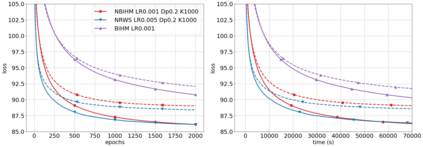
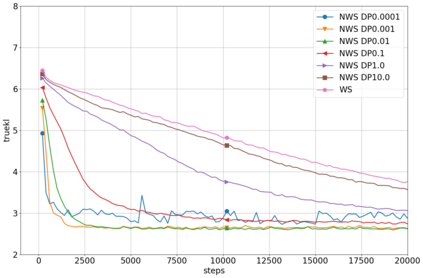
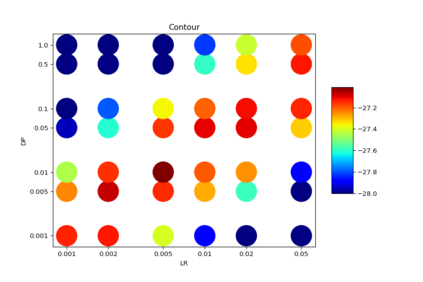
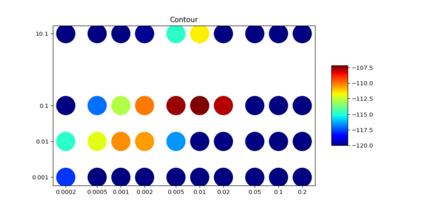
Helmholtz Machines (HMs) are a class of generative models composed of two Sigmoid Belief Networks (SBNs), acting as an encoder and a decoder. These models are commonly trained using a two-step optimization algorithm called Wake-Sleep (WS) and more recently by improved versions, such as Reweighted Wake-Sleep (RWS) and Bidirectional Helmholtz Machines (BiHM). The locality of the connections in an SBN induces sparsity in the Fisher information matrix associated to the model, in the form of a finely-grained block-diagonal structure. In this paper we exploit this property to efficiently train SBNs and HMs using the natural gradient. We present a novel algorithm called Natural Reweighted Wake-Sleep (NRWS), which corresponds to a geometric adaptation of the Reweighted Wake-Sleep, where, differently from most of the previous work, the natural gradient is computed without the need of introducing any approximation of the structure of the Fisher information matrix. The experiments performed on standard datasets from the literature show a consistent improvement of NRWS not only with respect to its non-geometric baseline but also with respect to state-of-the-art training algorithms for HMs. The improvement is quantified both in terms of speed of convergence as well as value of the log-likelihood reached after training.
翻译:Helmholtz Machines(HMS)是一组基因模型,由两个Sigmosublic Liision Lisis 网络(SBNs)组成,作为编码器和解码器。这些模型通常使用称为Wake-Sleep(WS)的两步优化算法来训练,最近则采用改良版本来训练,如Rews-Sleep(RWS)和Bidirectionalal Helmholtz Machines(BiHM)等。SBN的连接位置使与该模型相关的渔业信息矩阵的趋同性松散,其形式是精细的区块对面结构结构结构。在本文中,我们利用这一属性来利用自然梯度来有效训练SBNMs和HMs(HMs) 。我们介绍称为自然再加权休醒(RWS) (NWS) (RIS) (RIS) (RIS) (RIS) 的新算算法,这与大多数工作不同,在计算自然梯度的计算中,无需采用任何对渔业信息矩阵信息矩阵结构的近近近近度,但在矩阵结构结构结构。在标准上进行的实验,但从不光值改进也以其基准的逻辑上,在标准上进行不只标定的改进。