Bayesian inference of microbiota systems from count metagenomic data

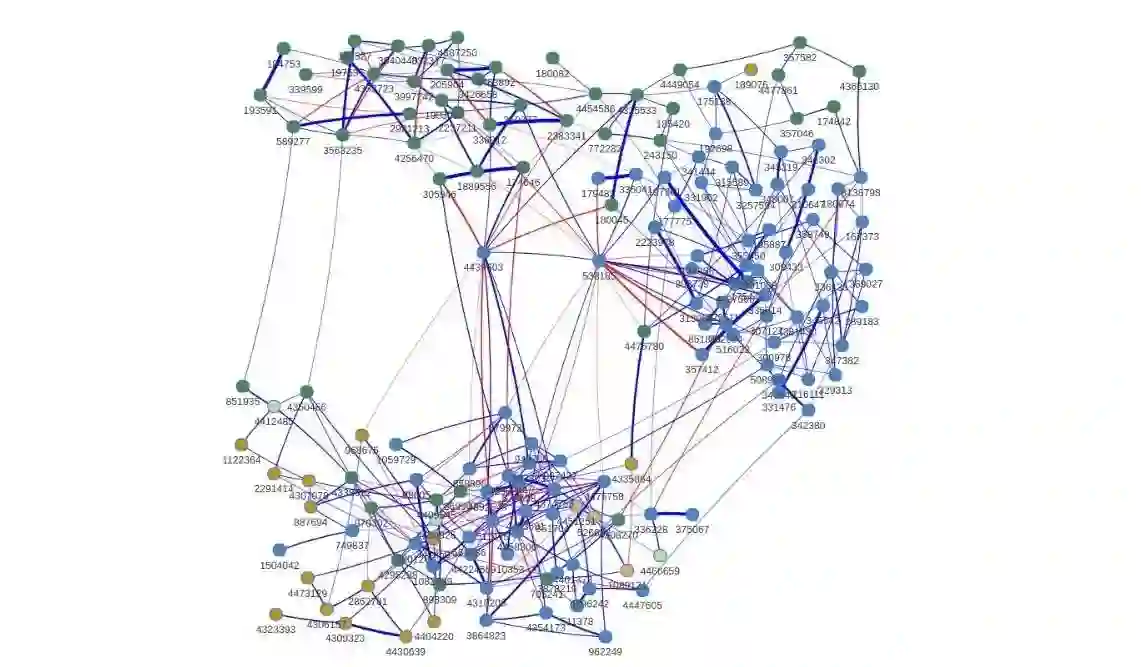
Metagenomics combined with high-resolution sequencing have enabled researchers to study the genomes of entire microbial communities. Revealing the underlying interactions between these communities is of vital importance to learn how microbes influence human health. Learning these interactions from microbiome data is challenging, due to the high dimensionality, discreteness, broad dispersion levels, compositionality and excess of zero counts that characterize these data. To tackle these issues, we develop a novel Gaussian copula graphical model with two key elements. Firstly, we model the marginal distributions via discrete Weibull regression, both to account for the typical features of microbiome data and to include the dependency from external covariates, often available in genomic studies but rarely used for network inference. Secondly, we advance a Bayesian structure learning framework, based on a computationally efficient search algorithm that is suited to high dimensionality. The approach returns simultaneous inference of the marginal effects and of the dependency structure, including graph uncertainty estimates. A simulation study and a real data analysis of microbiome data highlight the applicability of the proposed approach at inferring networks from high-dimensional count data in general, and its relevance to microbiota data analyses in particular. The proposed method is implemented in the R package BDgraph.