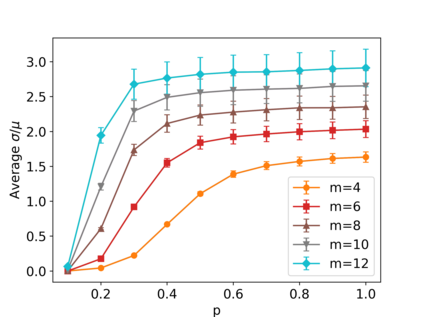
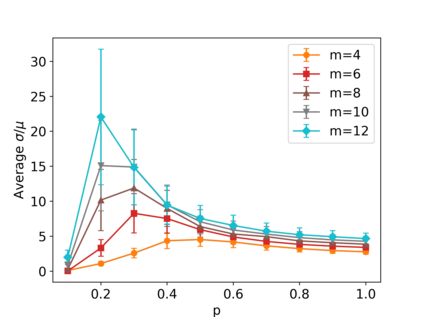
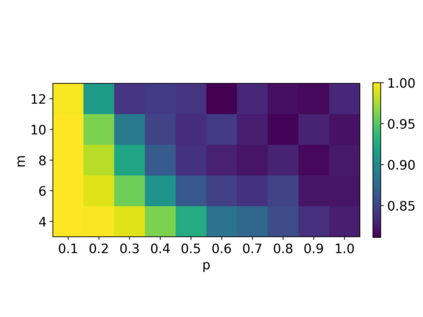
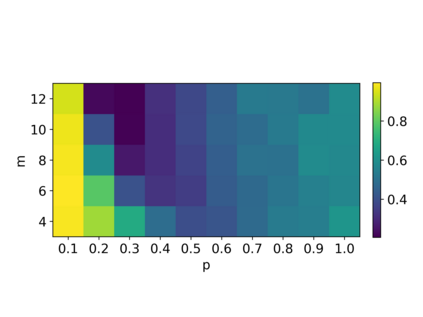
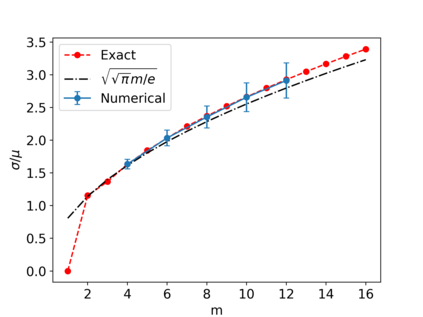
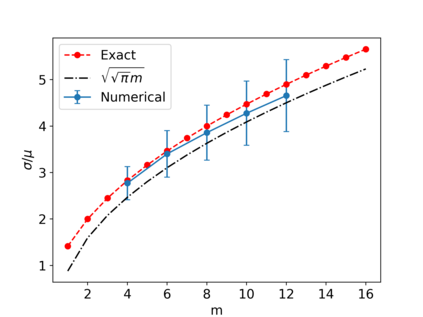
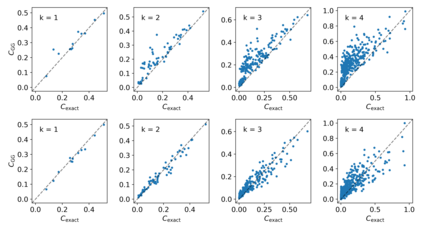
Gaussian Boson Samplers aim to demonstrate quantum advantage by performing a sampling task believed to be classically hard. The probabilities of individual outcomes in the sampling experiment are determined by the Hafnian of an appropriately constructed symmetric matrix. For nonnegative matrices, there is a family of randomized estimators of the Hafnian based on generating a particular random matrix and calculating its determinant. While these estimators are unbiased (the mean of the determinant is equal to the Hafnian of interest), their variance may be so high as to prevent an efficient estimation. Here we investigate the performance of two such estimators, which we call the Barvinok and Godsil-Gutman estimators. We find that in general both estimators perform well for adjacency matrices of random graphs, demonstrating a slow growth of variance with the size of the problem. Nonetheless, there are simple examples where both estimators show high variance, requiring an exponential number of samples. In addition, we calculate the asymptotic behavior of the variance for the complete graph. Finally, we simulate the Gaussian Boson Sampling using the Godsil-Gutman estimator and show that this technique can successfully reproduce low-order correlation functions.
翻译:暂无翻译