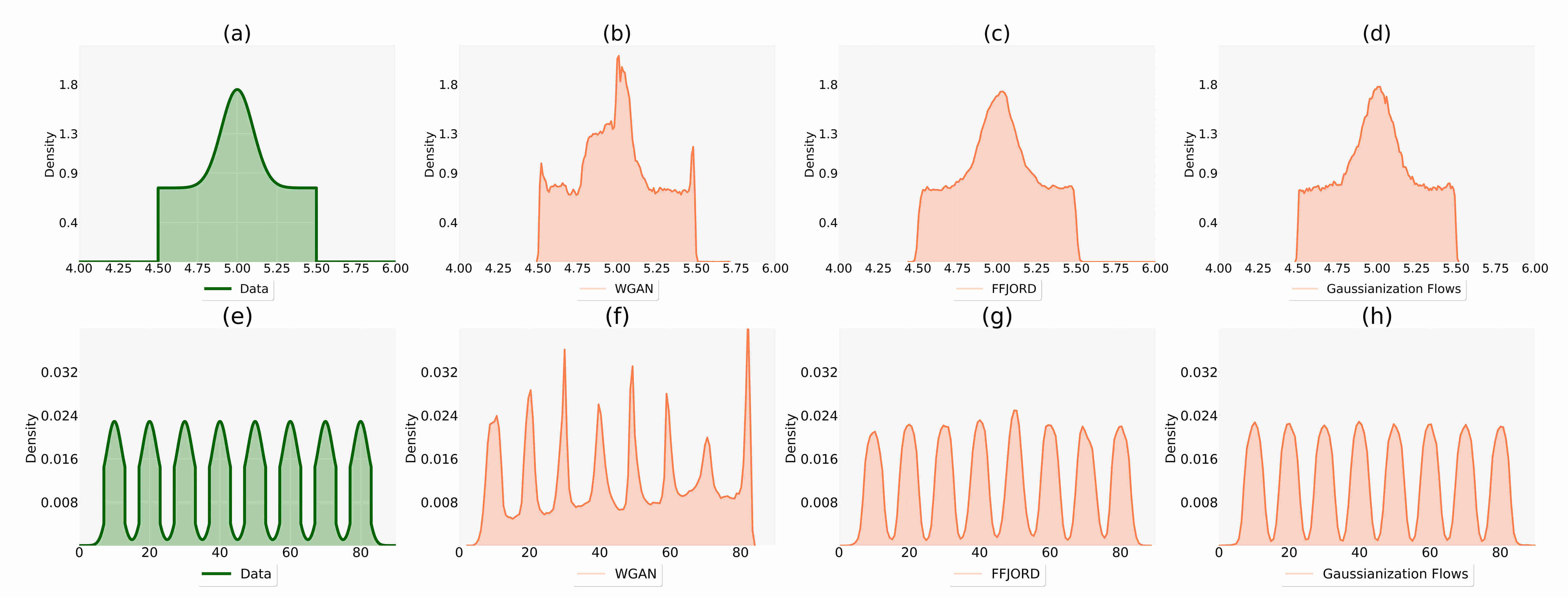
Generative adversarial networks (GANs) and normalizing flows are both approaches to density estimation that use deep neural networks to transform samples from an uninformative prior distribution to an approximation of the data distribution. There is great interest in both for general-purpose statistical modeling, but the two approaches have seldom been compared to each other for modeling non-image data. The difficulty of computing likelihoods with GANs, which are implicit models, makes conducting such a comparison challenging. We work around this difficulty by considering several low-dimensional synthetic datasets. An extensive grid search over GAN architectures, hyperparameters, and training procedures suggests that no GAN is capable of modeling our simple low-dimensional data well, a task we view as a prerequisite for an approach to be considered suitable for general-purpose statistical modeling. Several normalizing flows, on the other hand, excelled at these tasks, even substantially outperforming WGAN in terms of Wasserstein distance -- the metric that WGAN alone targets. Scientists and other practitioners should be wary of relying on WGAN for applications that require accurate density estimation.
翻译:生成对抗性网络(GANs)和正常流动是密度估计方法,它们使用深神经网络将样本从未提供信息的先前分布方式转换为数据分布近似值。对通用统计模型都非常感兴趣,但这两种方法很少为非图像数据建模相互比较。与隐含模型的GANs计算可能性的困难使得进行这种比较具有挑战性。我们通过考虑几个低维合成数据集来克服这一困难。在GAN结构、超参数和培训程序上进行广泛的网格搜索表明,没有一个GAN能够模拟我们简单的低维度数据,我们认为这是一项任务是被视为适合通用统计模型的方法的先决条件。另一方面,一些标准化的流程在这些任务上甚至大大超过WGAN的瓦森施泰尔距离 -- -- 这个尺度是WGAN单独的目标。科学家和其他从业人员应当谨慎地依赖WGAN进行需要准确密度估计的应用。