Pointer Graph Networks

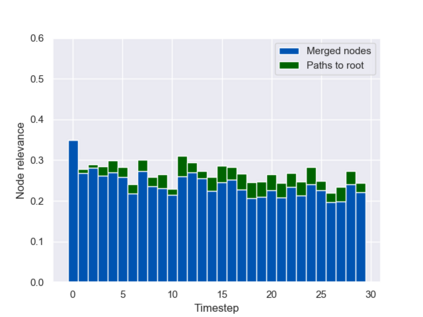
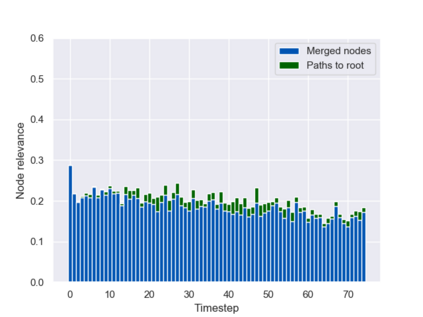
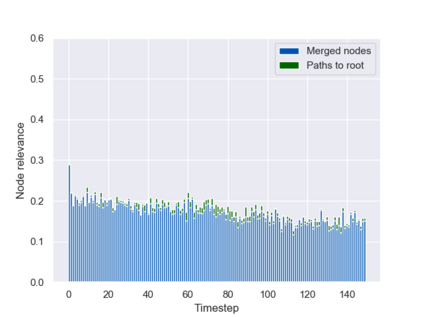
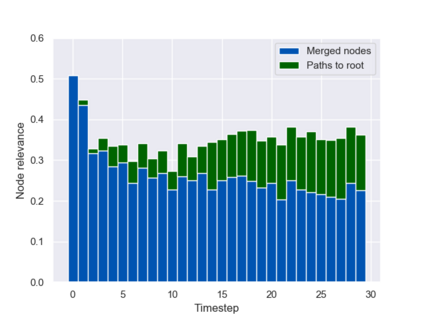
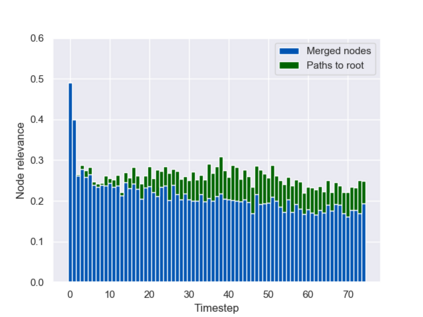
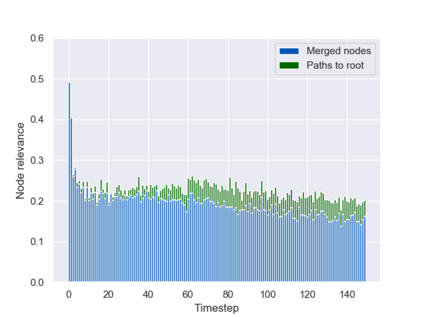
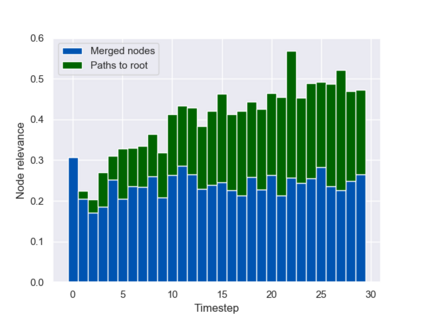
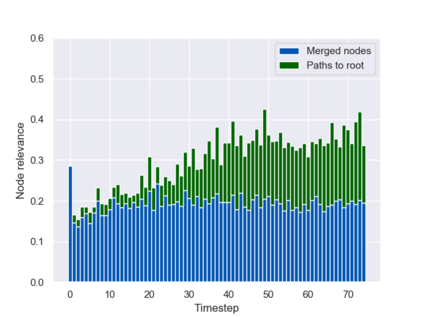
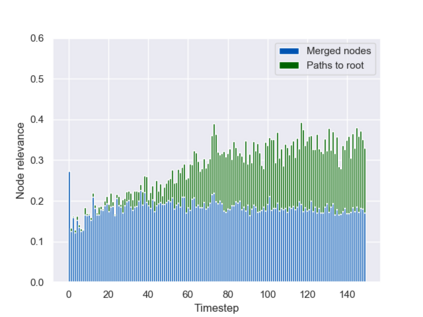
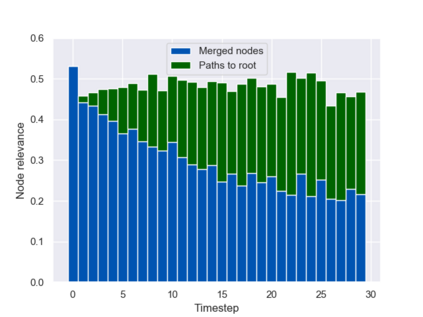
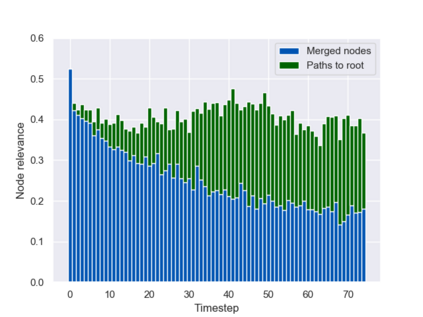
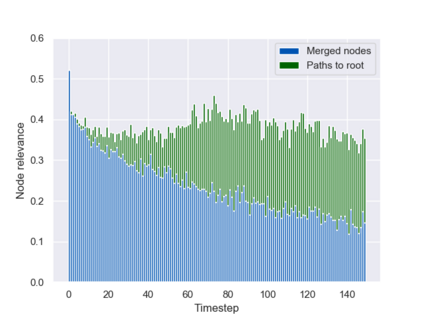
Graph neural networks (GNNs) are typically applied to static graphs that are assumed to be known upfront. This static input structure is often informed purely by insight of the machine learning practitioner, and might not be optimal for the actual task the GNN is solving. In absence of reliable domain expertise, one might resort to inferring the latent graph structure, which is often difficult due to the vast search space of possible graphs. Here we introduce Pointer Graph Networks (PGNs) which augment sets or graphs with additional inferred edges for improved model expressivity. PGNs allow each node to dynamically point to another node, followed by message passing over these pointers. The sparsity of this adaptable graph structure makes learning tractable while still being sufficiently expressive to simulate complex algorithms. Critically, the pointing mechanism is directly supervised to model long-term sequences of operations on classical data structures, incorporating useful structural inductive biases from theoretical computer science. Qualitatively, we demonstrate that PGNs can learn parallelisable variants of pointer-based data structures, namely disjoint set unions and link/cut trees. PGNs generalise out-of-distribution to 5x larger test inputs on dynamic graph connectivity tasks, outperforming unrestricted GNNs and Deep Sets.