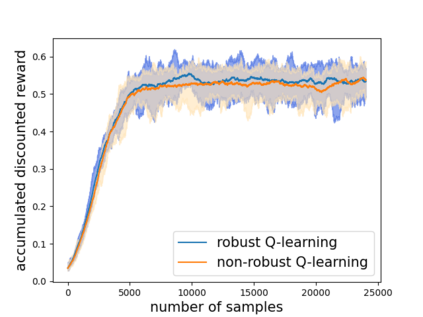
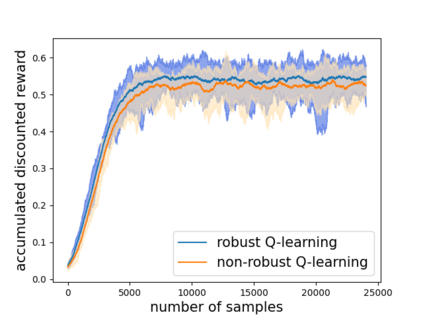
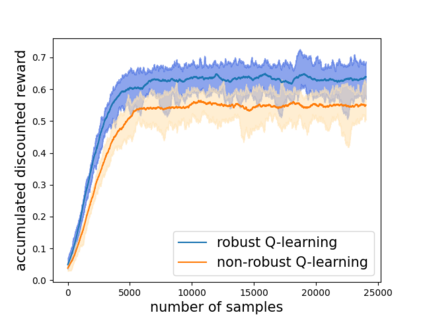
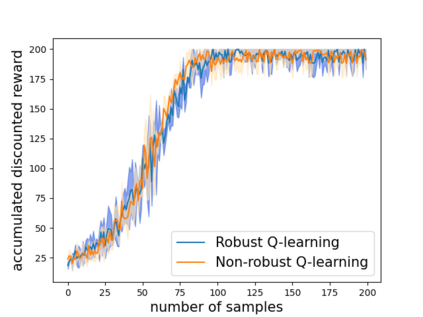
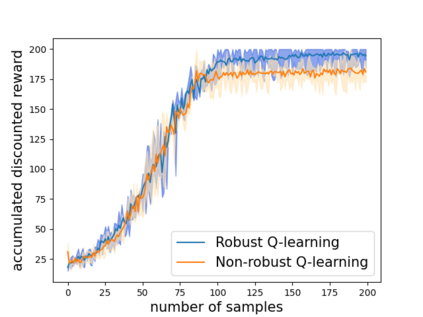
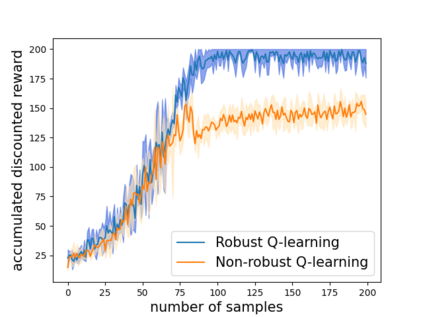
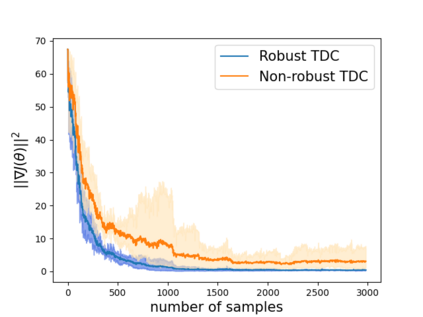
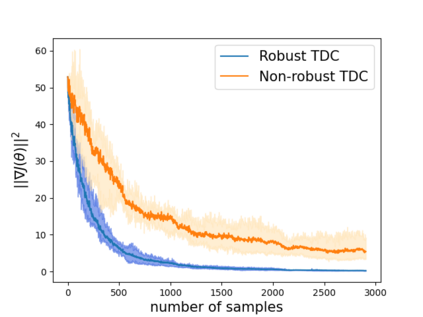
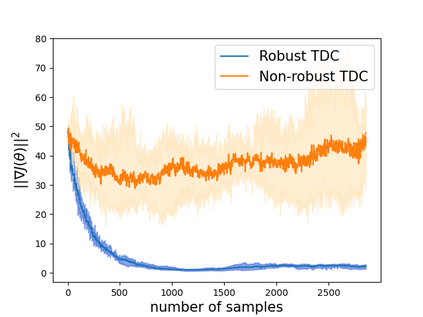
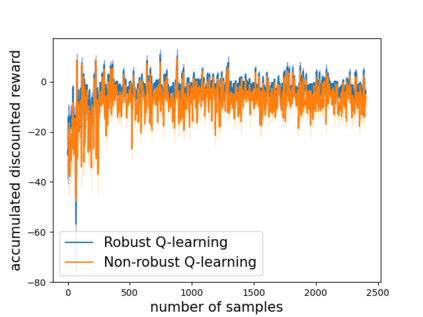
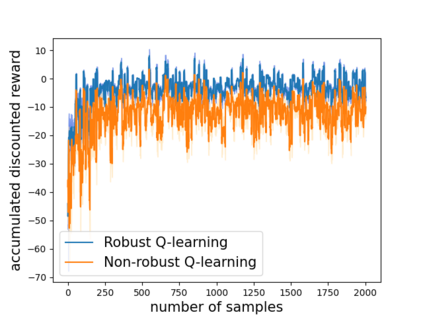
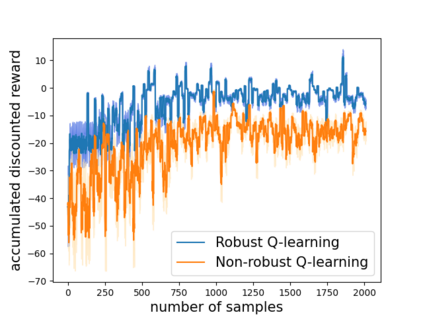
Robust reinforcement learning (RL) is to find a policy that optimizes the worst-case performance over an uncertainty set of MDPs. In this paper, we focus on model-free robust RL, where the uncertainty set is defined to be centering at a misspecified MDP that generates a single sample trajectory sequentially and is assumed to be unknown. We develop a sample-based approach to estimate the unknown uncertainty set and design a robust Q-learning algorithm (tabular case) and robust TDC algorithm (function approximation setting), which can be implemented in an online and incremental fashion. For the robust Q-learning algorithm, we prove that it converges to the optimal robust Q function, and for the robust TDC algorithm, we prove that it converges asymptotically to some stationary points. Unlike the results in [Roy et al., 2017], our algorithms do not need any additional conditions on the discount factor to guarantee the convergence. We further characterize the finite-time error bounds of the two algorithms and show that both the robust Q-learning and robust TDC algorithms converge as fast as their vanilla counterparts(within a constant factor). Our numerical experiments further demonstrate the robustness of our algorithms. Our approach can be readily extended to robustify many other algorithms, e.g., TD, SARSA, and other GTD algorithms.
翻译:强力强化学习( RL) 是找到一种政策, 优化最坏的绩效, 而不是一个 MDP 的不确定性。 在本文中, 我们侧重于一个没有模型的稳健 RL, 不确定性组被定义为以一个错误指定的 MDP为中心, 并按顺序生成单一样本轨迹, 并假定是未知的。 我们开发了一个基于样本的办法来估计未知的不确定性组, 并设计一个强大的 Q- 学习算法( tabilor case) 和强大的 TDC 算法( 功能近似设置), 可以在线和递增方式实施。 对于强大的 Q- 学习算法, 我们证明它与最强的 Q 函数相融合, 而对于强大的 TDC 算法, 我们证明它与某些固定点相融合。 与 [ Roy et al. 2017] 的结果不同, 我们的算法不需要在折扣系数上附加任何条件来保证趋同。 我们进一步描述两种算法的有限时间误差, 并显示强大的 Q- 和强大的 电子算算法能够快速的同步地归结为我们的其他 的 。