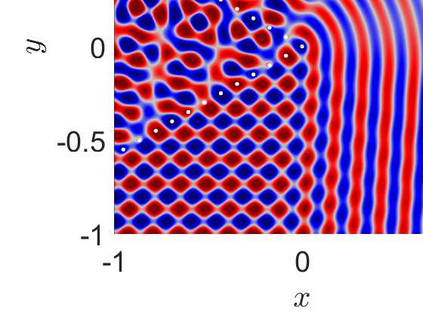
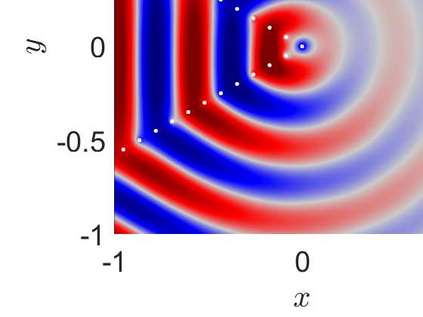
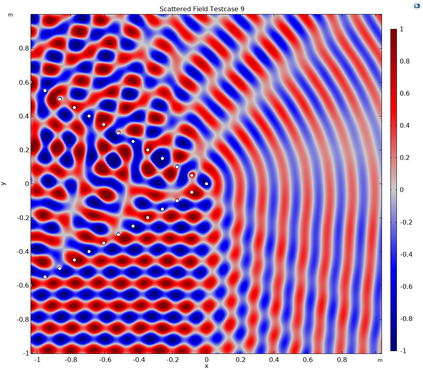
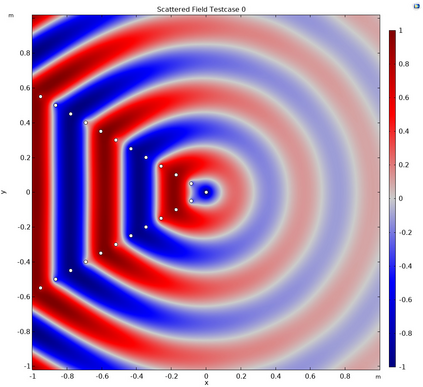
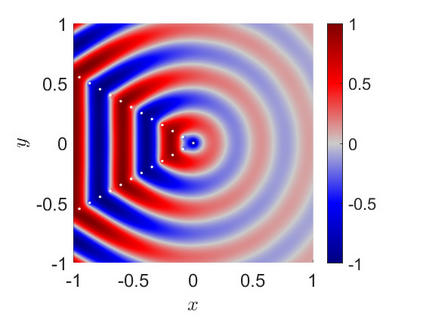
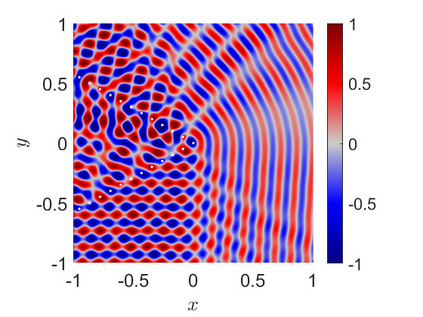
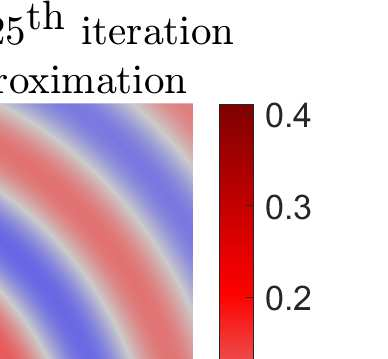
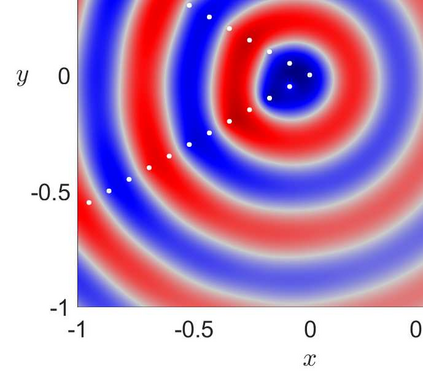
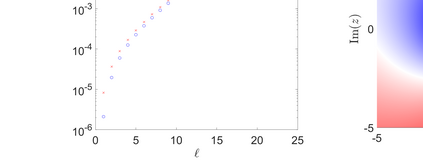
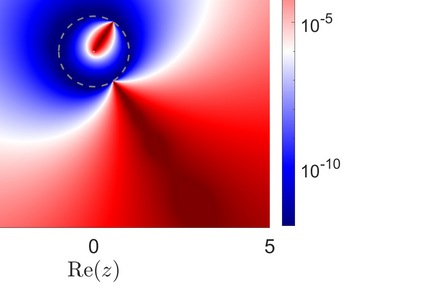
This article considers the problem of diffraction by a wedge consisting of two semi-infinite periodic arrays of point scatterers. The solution is obtained in terms of two coupled systems, each of which is solved using the discrete Wiener--Hopf technique. An effective and accurate iterative numerical procedure is developed to solve the diffraction problem, which allows us to compute the interaction of thousands of scatterers forming the wedge. A crucial aspect of this numerical procedure is the effective truncation of slowly convergent single and double infinite series, which requires careful asymptotic analysis. A convergence criteria is formulated and shown to be satisfied for a large class of physically interesting cases. A comparison to direct numerical simulations is made, highlighting the accuracy of the method.
翻译:本条考虑了由两组半无限定期的点散射器组成的介面的折射问题。 解决办法来自两个组合系统, 每一个系统都使用离散 Wiener- Hopf 技术解决。 开发了一个有效和准确的迭代数字程序来解决折射问题, 从而使我们能够计算成介面的数千个散射器的相互作用。 这个数字程序的一个关键方面是缓慢趋同的单项和双倍无限序列的有效截断, 这需要谨慎的零星分析。 一种趋同标准被制定出来, 并显示能够满足一大批实际有趣的案例。 与直接的数字模拟进行比较, 突出方法的准确性 。