The Helmholtz problem in slowly varying waveguides at locally resonant frequencies

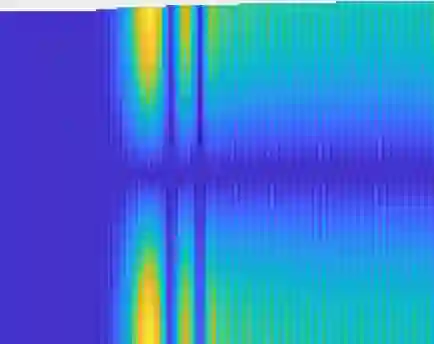
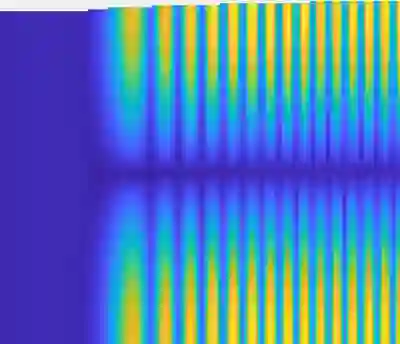
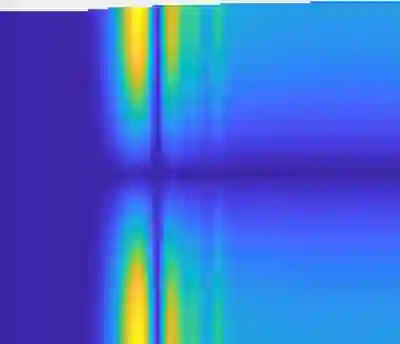
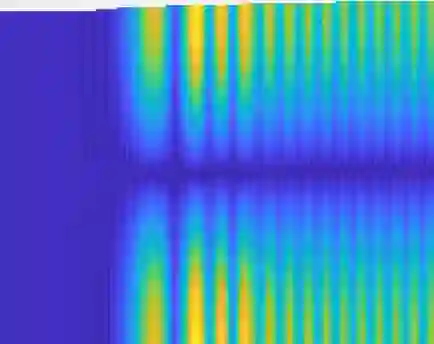
This article aims to present a general study of the Helmholtz problem in slowly varying waveguides. This work is of particular interest at locally resonant frequencies, where a phenomenon close to the tunnel effect for Schr\"odinger equation in quantum mechanics can be observed. In this situation, locally resonant modes propagate in the waveguide under the form of Airy functions. Using previous mathematical results on the Schr\"odinger equation, we prove the existence of a unique solution to the Helmholtz source problem with outgoing conditions in such waveguides. We provide an explicit modal approximation of this solution, as well as a control of the approximation error in H1loc. The main theorem is proved in the case of a waveguide with a monotonously varying profile and then generalized using a matching strategy. We finally validate the modal approximation by comparing it to numerical solutions based on the finite element method.