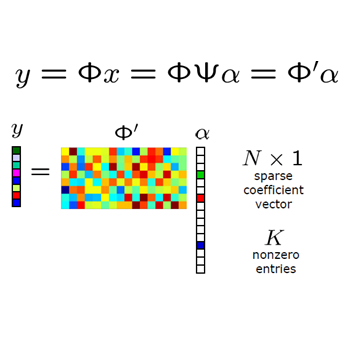
We study an auto-calibration problem in which a transform-sparse signal is compressive-sensed by multiple sensors in parallel with unknown sensing parameters. The problem has an important application in pMRI reconstruction, where explicit coil calibrations are often difficult and costly to achieve in practice, but nevertheless a fundamental requirement for high-precision reconstructions. Most auto-calibrated strategies result in reconstruction that corresponds to solving a challenging biconvex optimization problem. We transform the auto-calibrated parallel sensing as a convex optimization problem using the idea of `lifting'. By exploiting sparsity structures in the signal and the redundancy introduced by multiple sensors, we solve a mixed-norm minimization problem to recover the underlying signal and the sensing parameters simultaneously. Robust and stable recovery guarantees are derived in the presence of noise and sparsity deficiencies in the signals. For the pMRI application, our method provides a theoretically guaranteed approach to self-calibrated parallel imaging to accelerate MRI acquisitions under appropriate assumptions. Developments in MRI are discussed, and numerical simulations using the analytical phantom and simulated coil sensitives are presented to support our theoretical results.
翻译:暂无翻译