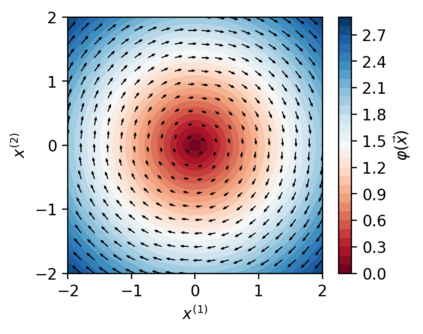
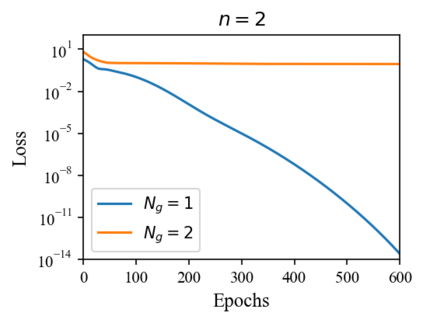
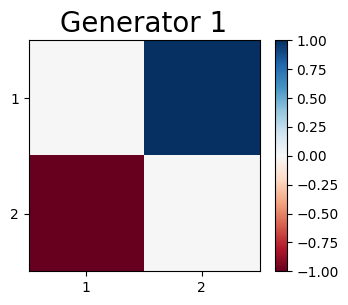
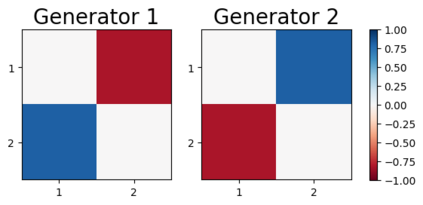
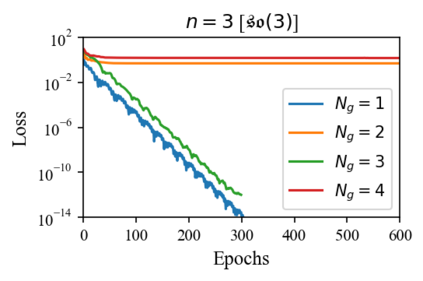
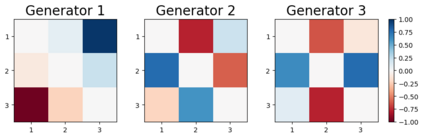
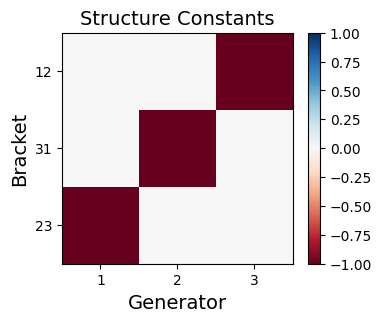
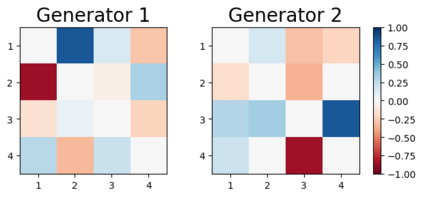
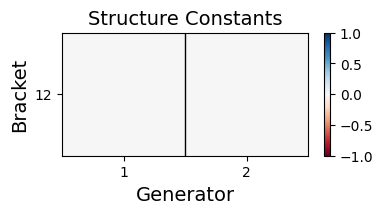
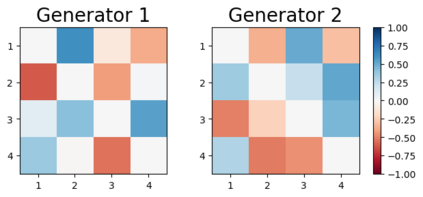
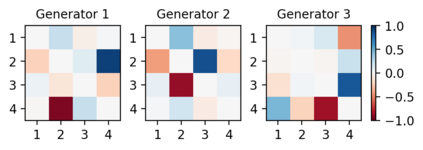
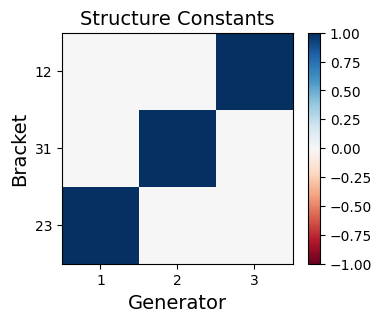
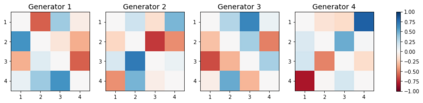
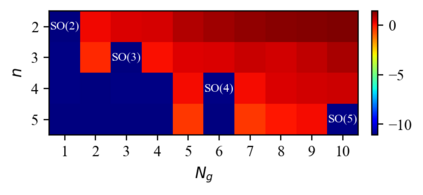
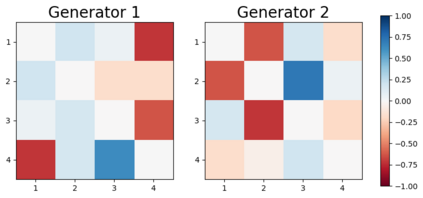
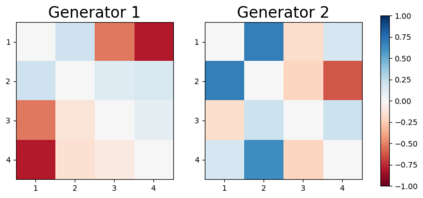
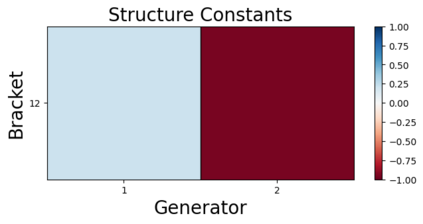
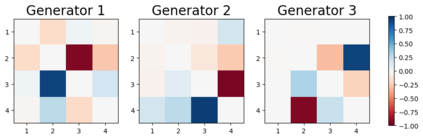
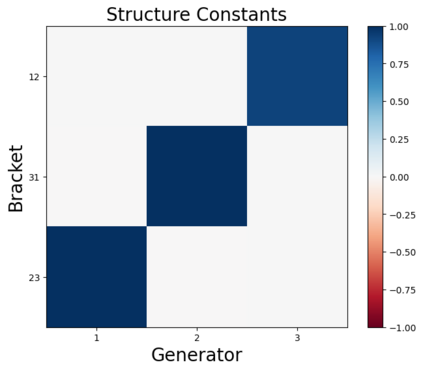
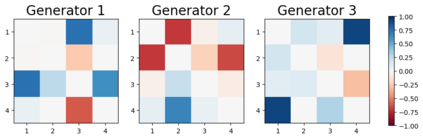
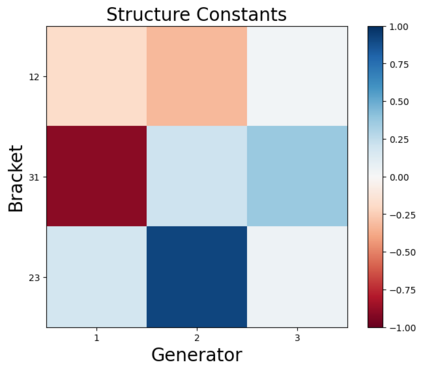
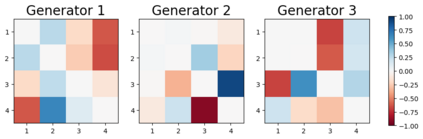
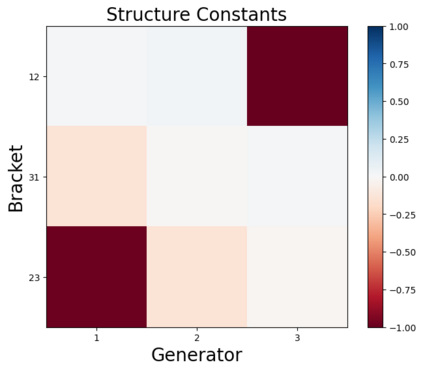
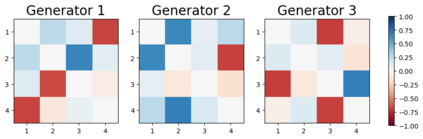
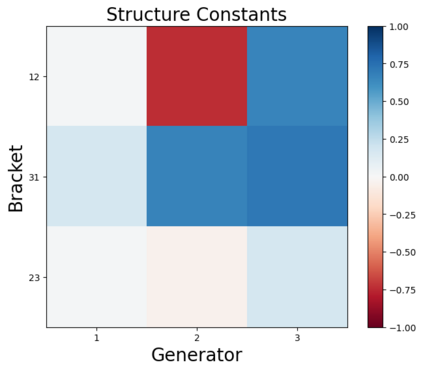
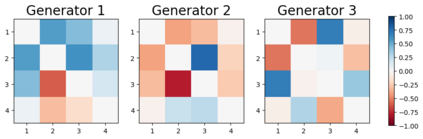
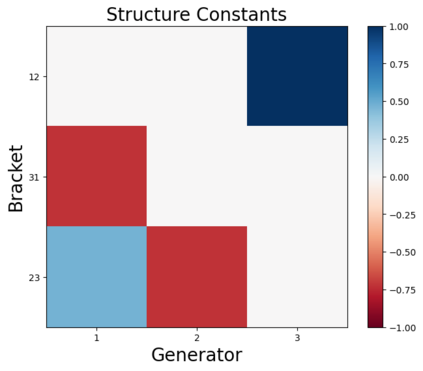
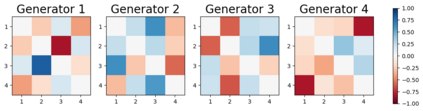
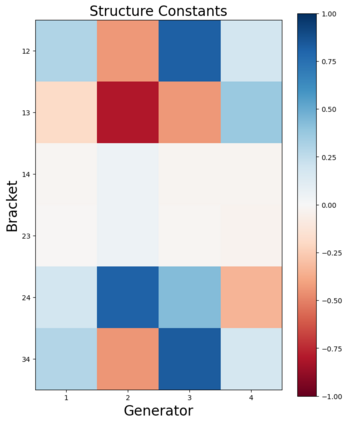
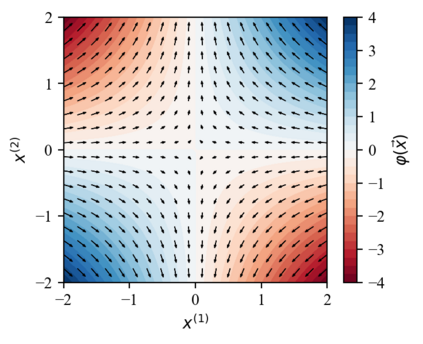
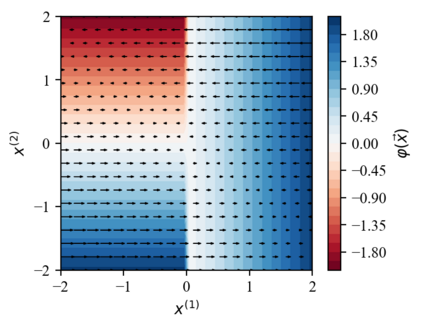
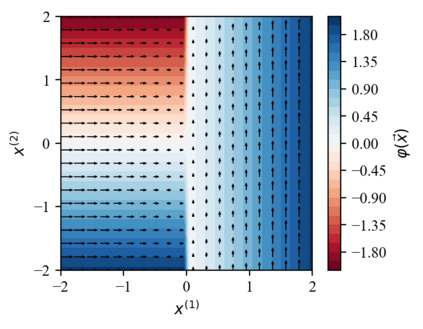
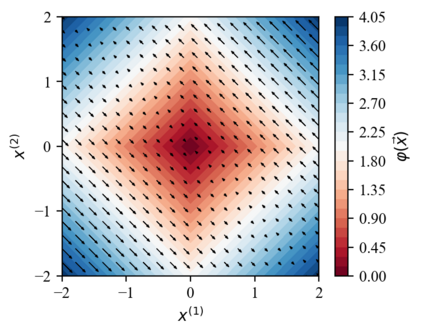
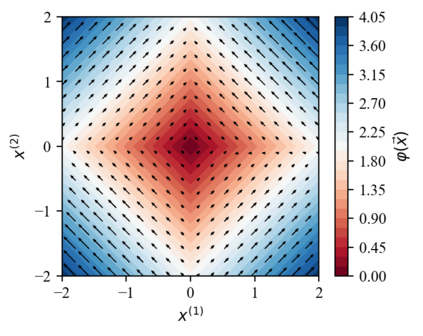
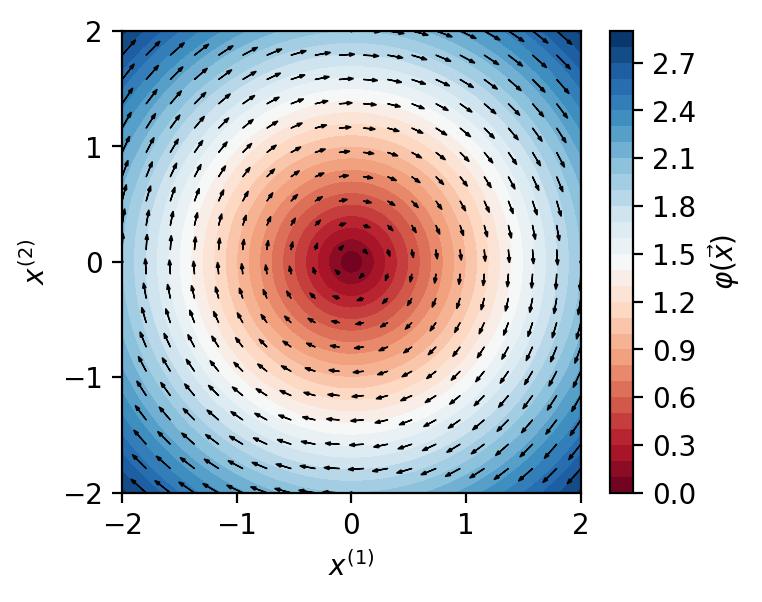
We design a deep-learning algorithm for the discovery and identification of the continuous group of symmetries present in a labeled dataset. We use fully connected neural networks to model the symmetry transformations and the corresponding generators. We construct loss functions that ensure that the applied transformations are symmetries and that the corresponding set of generators forms a closed (sub)algebra. Our procedure is validated with several examples illustrating different types of conserved quantities preserved by symmetry. In the process of deriving the full set of symmetries, we analyze the complete subgroup structure of the rotation groups $SO(2)$, $SO(3)$, and $SO(4)$, and of the Lorentz group $SO(1,3)$. Other examples include squeeze mapping, piecewise discontinuous labels, and $SO(10)$, demonstrating that our method is completely general, with many possible applications in physics and data science. Our study also opens the door for using a machine learning approach in the mathematical study of Lie groups and their properties.
翻译:我们为发现和识别标签数据集中存在的连续对称群设计了一个深学习算法,我们使用完全连接的神经网络模拟对称变换和相应的发电机,我们建造了损失功能,确保应用变换是对称的,相应的发电机组构成封闭的(子)变相。我们的程序通过几个例子来验证,说明通过对称保存的不同种类的养护量。在计算整套对称的进程中,我们分析了旋转组(USO(2)美元、USO(3)美元和USSO(4)美元)和Lorentz组(1,3,3美元)的完整分组结构。其他例子包括挤压绘图、片断性断性标签和$SO(10)美元,表明我们的方法是完全通用的,在物理和数据科学方面有许多可能的应用。我们的研究还打开了在对 Lie组及其特性的数学研究中使用机器学习方法的大门。