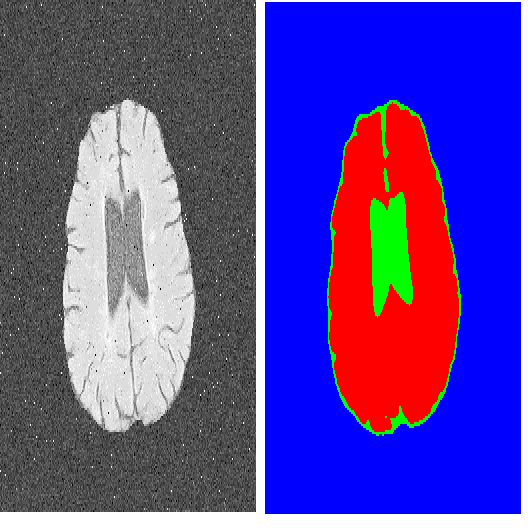
With the inspiration of vision transformers, the concept of depth-wise convolution revisits to provide a large Effective Receptive Field (ERF) using Large Kernel (LK) sizes for medical image segmentation. However, the segmentation performance might be saturated and even degraded as the kernel sizes scaled up (e.g., $21\times 21\times 21$) in a Convolutional Neural Network (CNN). We hypothesize that convolution with LK sizes is limited to maintain an optimal convergence for locality learning. While Structural Re-parameterization (SR) enhances the local convergence with small kernels in parallel, optimal small kernel branches may hinder the computational efficiency for training. In this work, we propose RepUX-Net, a pure CNN architecture with a simple large kernel block design, which competes favorably with current network state-of-the-art (SOTA) (e.g., 3D UX-Net, SwinUNETR) using 6 challenging public datasets. We derive an equivalency between kernel re-parameterization and the branch-wise variation in kernel convergence. Inspired by the spatial frequency in the human visual system, we extend to vary the kernel convergence into element-wise setting and model the spatial frequency as a Bayesian prior to re-parameterize convolutional weights during training. Specifically, a reciprocal function is leveraged to estimate a frequency-weighted value, which rescales the corresponding kernel element for stochastic gradient descent. From the experimental results, RepUX-Net consistently outperforms 3D SOTA benchmarks with internal validation (FLARE: 0.929 to 0.944), external validation (MSD: 0.901 to 0.932, KiTS: 0.815 to 0.847, LiTS: 0.933 to 0.949, TCIA: 0.736 to 0.779) and transfer learning (AMOS: 0.880 to 0.911) scenarios in Dice Score.
翻译:在视觉变异器的启发下, 深度- 直流变异概念 80 - 直流变异概念 80 - 直流变异概念, 以提供大型有效感知字段 。 但是, 当内核变异时, 内核变异( 例如, 21 - 21 - 21 - 21 - 21 美元 ), 断裂性表现可能会饱和甚至退化 。 我们假设, 与 LK 大小的变异有限, 以维持地方学习的最佳趋同 。 结构重新校正度变异( SR) 使本地与小内核内核变异( LKK) 趋同: 最佳小内核分流分流会阻碍培训的计算效率 。 在这项工作中, 我们提议 RepUX- Net, 纯CN 结构, 其简单大内核内核内核电离子变异( DITA) 模式, 3D- 直流- 直流- 直流流变异( 直流- 直流- 直流- 直流- 直流- 直流- 直流- 流- 流- 直流- 流- 直流- 流- 流- 流- 向- 向- 流- 流- 流- 流- 直流- 流- 直流- 流- 向- 向- 流- 流- 向- 流- 流- 流- 流- 流- 向- 向- 向- 向- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 向- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流-</s>