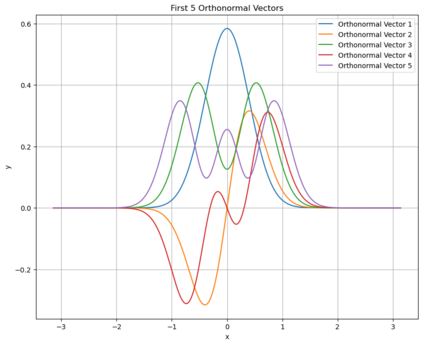
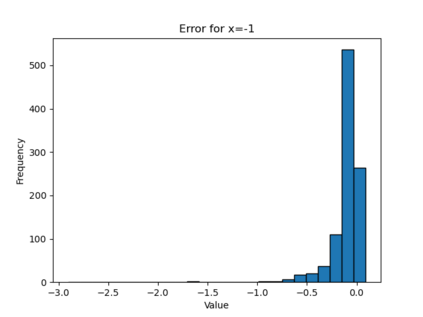
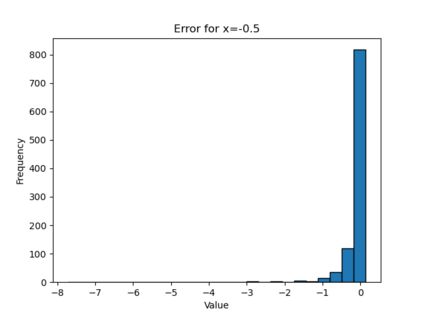
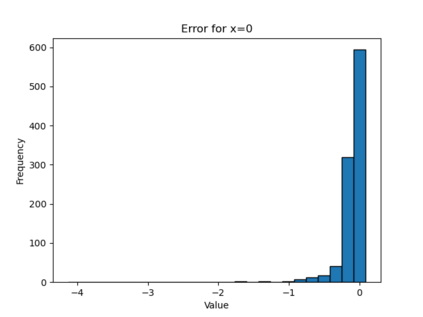
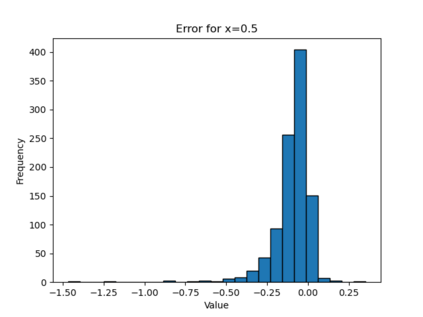
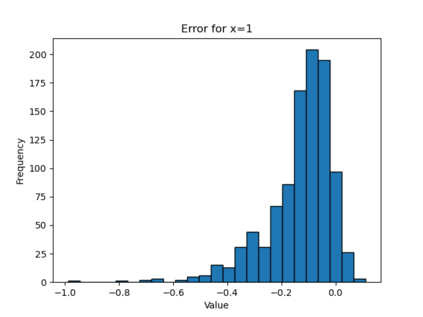
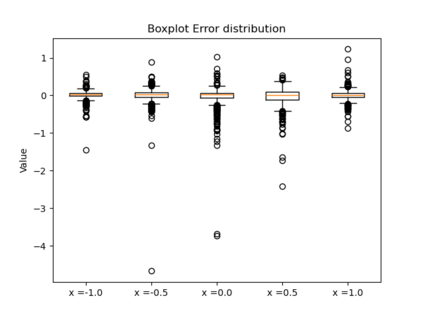
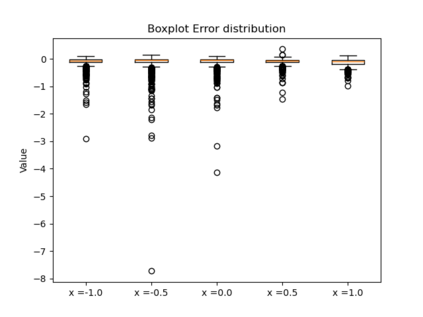
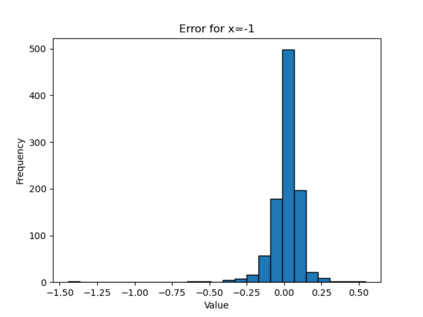
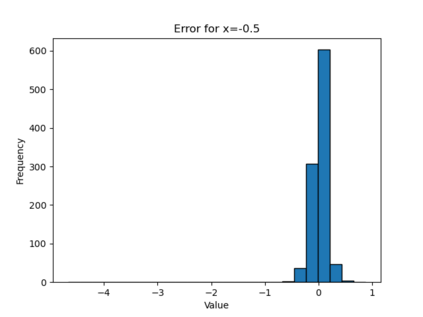
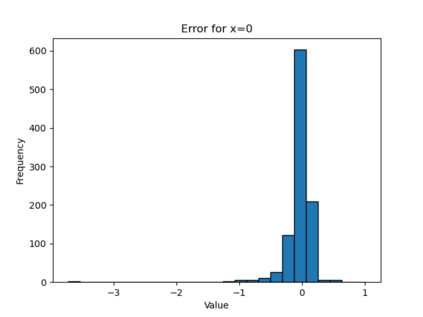
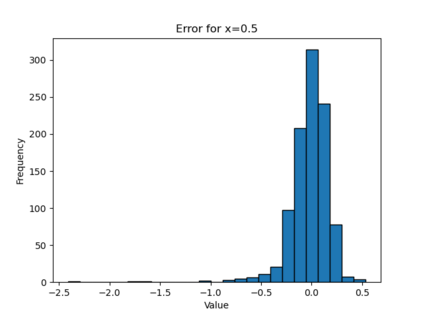
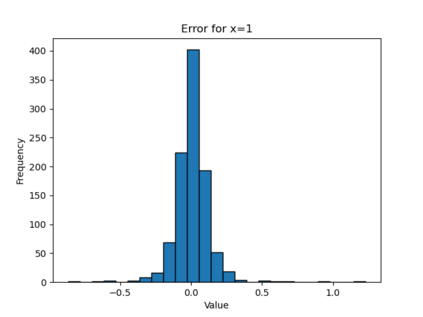
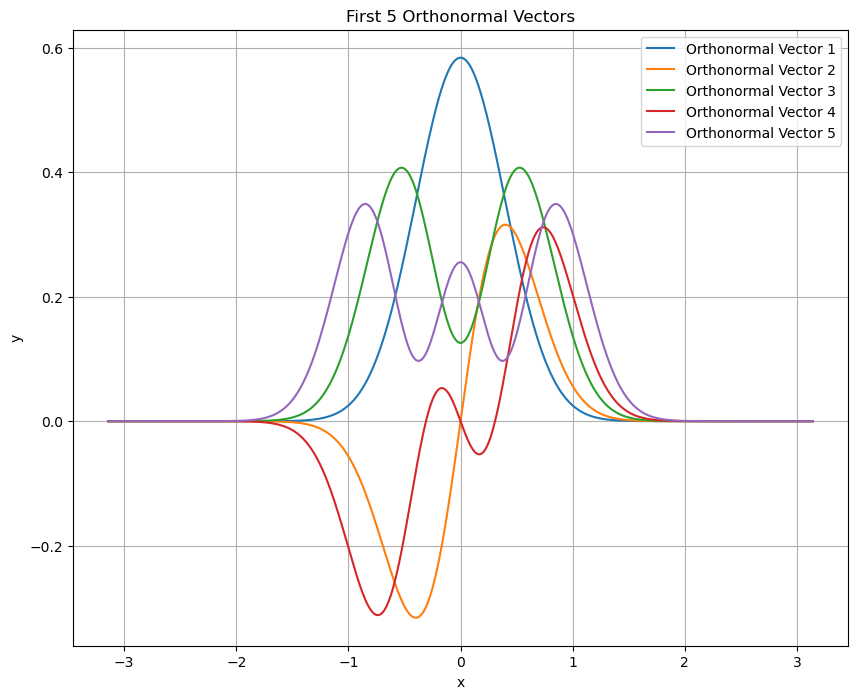
In this paper, we present a framework for learning the solution map of a backward parabolic Cauchy problem. The solution depends continuously but nonlinearly on the final data, source, and force terms, all residing in Banach spaces of functions. We utilize Fr\'echet space neural networks (Benth et al. (2023)) to address this operator learning problem. Our approach provides an alternative to Deep Operator Networks (DeepONets), using basis functions to span the relevant function spaces rather than relying on finite-dimensional approximations through censoring. With this method, structural information encoded in the basis coefficients is leveraged in the learning process. This results in a neural network designed to learn the mapping between infinite-dimensional function spaces. Our numerical proof-of-concept demonstrates the effectiveness of our method, highlighting some advantages over DeepONets.
翻译:暂无翻译