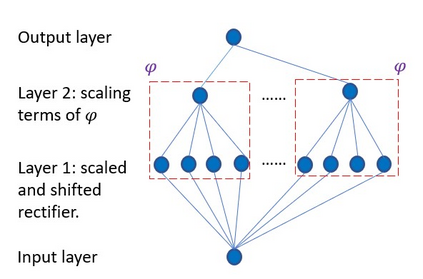
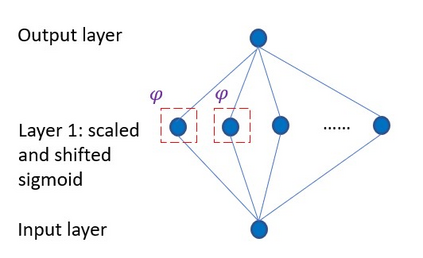
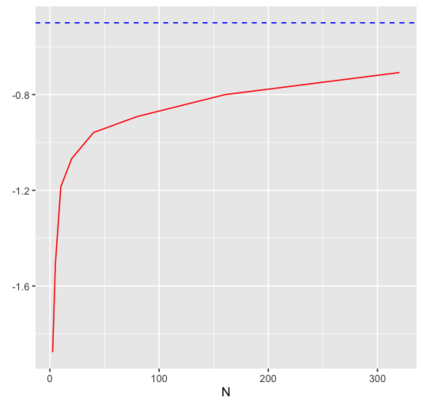
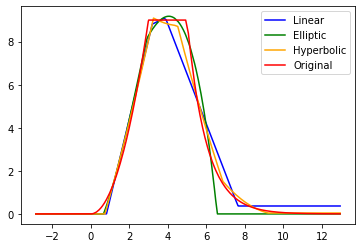
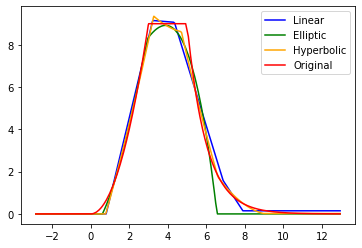
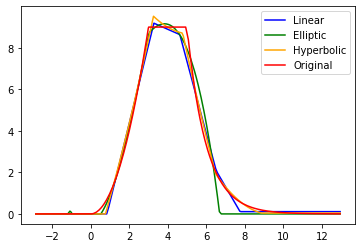
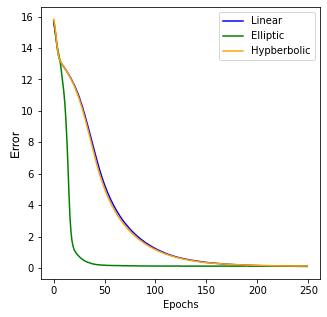
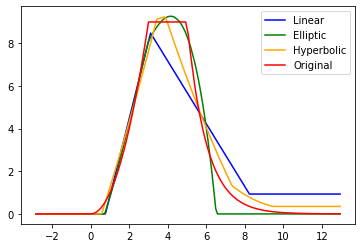
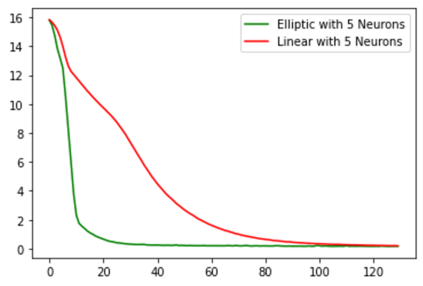
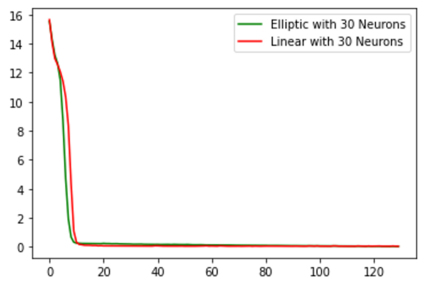
In this paper we propose a new class of neural network functions which are linear combinations of compositions of activation functions with quadratic functions, replacing standard affine linear functions, often called neurons. We show the universality of this approximation and prove convergence rates results based on the theory of wavelets and statistical learning. We investigate the efficiency of our new approach numerically for simple test cases, by showing that it requires less numbers of neurons that standard affine linear neural networks. Similar observations are made when comparing deep (multi-layer) networks.
翻译:在本文中,我们提出了一个新的神经网络功能类别,这些神经网络功能是激活功能组成与二次函数的线性组合,取代标准的直线功能,通常称为神经元。我们展示了这种近似的普遍性,并根据波子理论和统计学学习证明了趋同率的结果。我们用数字方法调查我们新的方法对简单测试案例的效率,方法是显示它需要较少的神经元来标准线性神经网络。在比较深层(多层)网络时,也做了类似的观察。