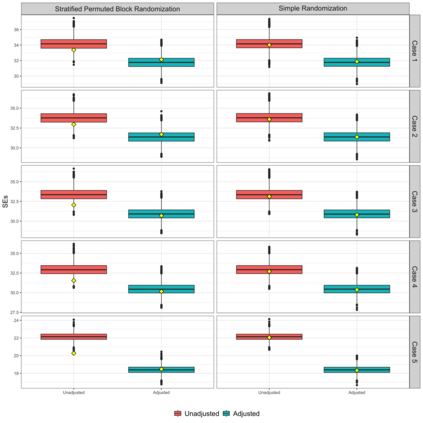
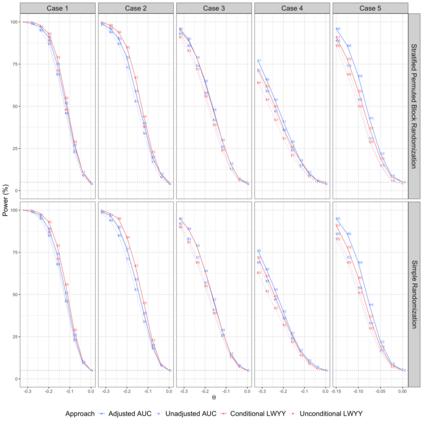
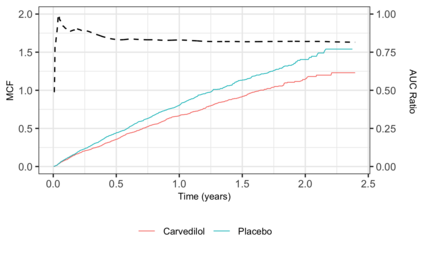
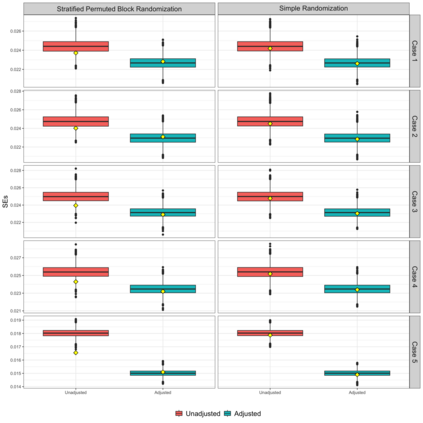
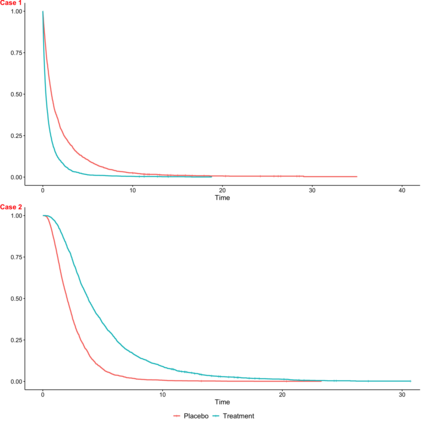
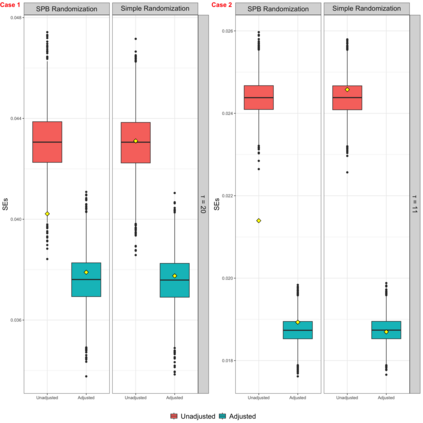
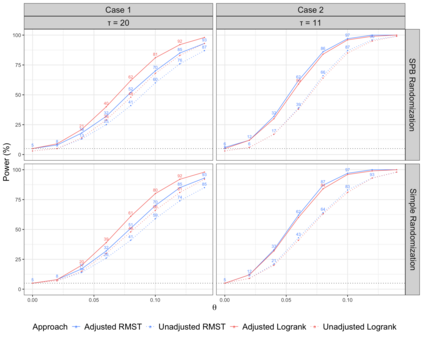
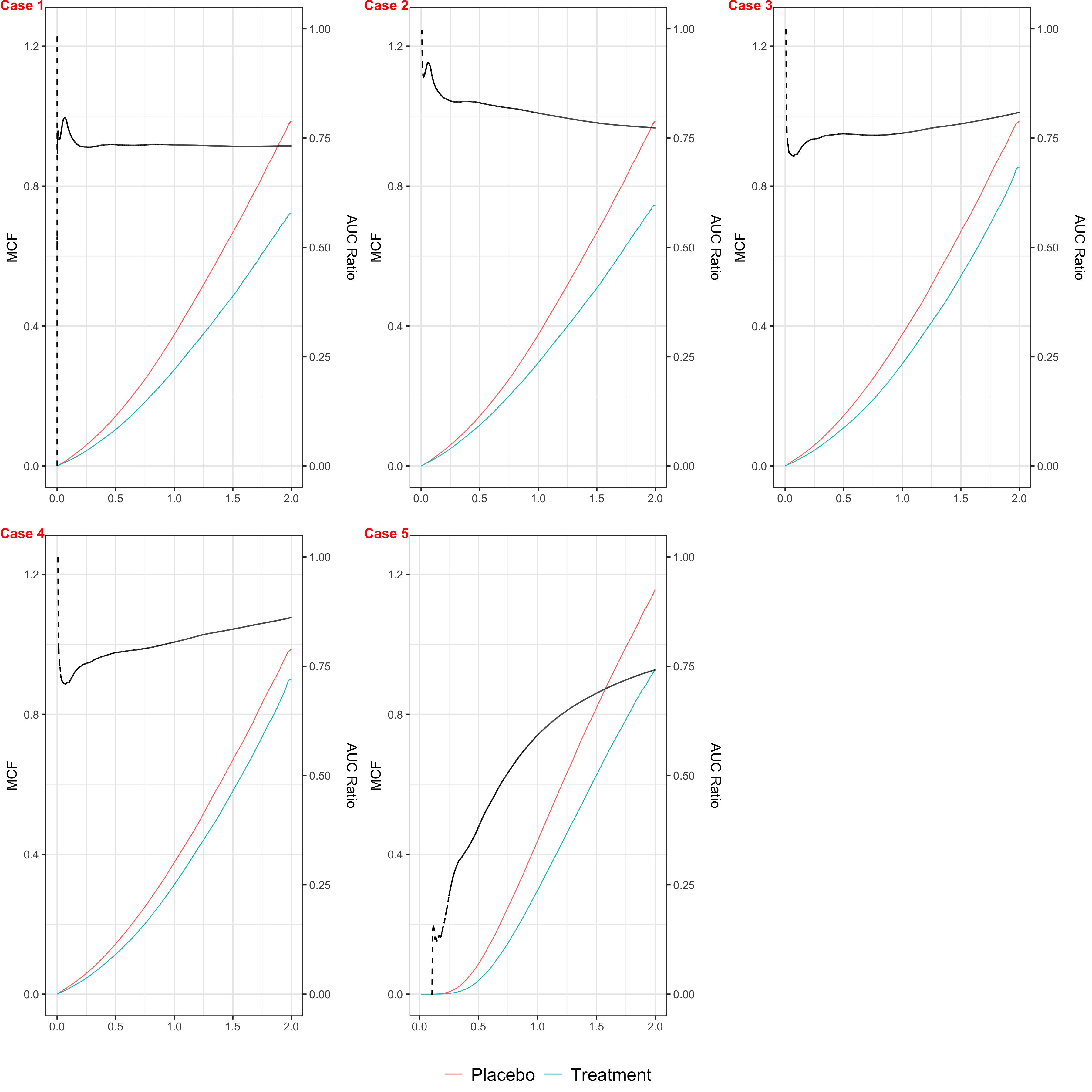
The area under the curve (AUC) of the mean cumulative function (MCF) has recently been introduced as a novel estimand for evaluating treatment effects in recurrent event settings, capturing a totality of evidence in relation to disease progression. While the Lin-Wei-Yang-Ying (LWYY) model is commonly used for analyzing recurrent events, it relies on the proportional rate assumption between treatment arms, which is often violated in practice. In contrast, the AUC under MCFs does not depend on such proportionality assumptions and offers a clinically interpretable measure of treatment effect. To improve the precision of the AUC estimation while preserving its unconditional interpretability, we propose a nonparametric covariate adjustment approach. This approach guarantees efficiency gain compared to unadjusted analysis, as demonstrated by theoretical asymptotic distributions, and is universally applicable to various randomization schemes, including both simple and covariate-adaptive designs. Extensive simulations across different scenarios further support its advantage in increasing statistical power. Our findings highlight the importance of covariate adjustment for the analysis of AUC in recurrent event settings, offering practical guidance for its application in randomized clinical trials.
翻译:暂无翻译