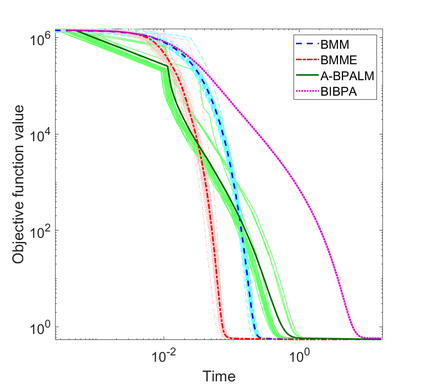
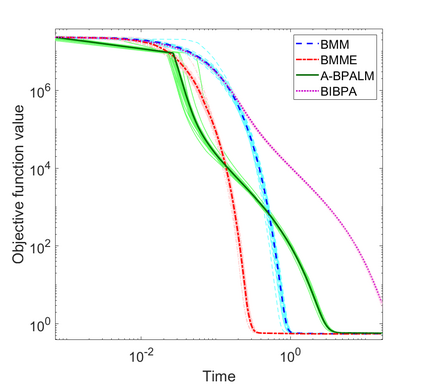
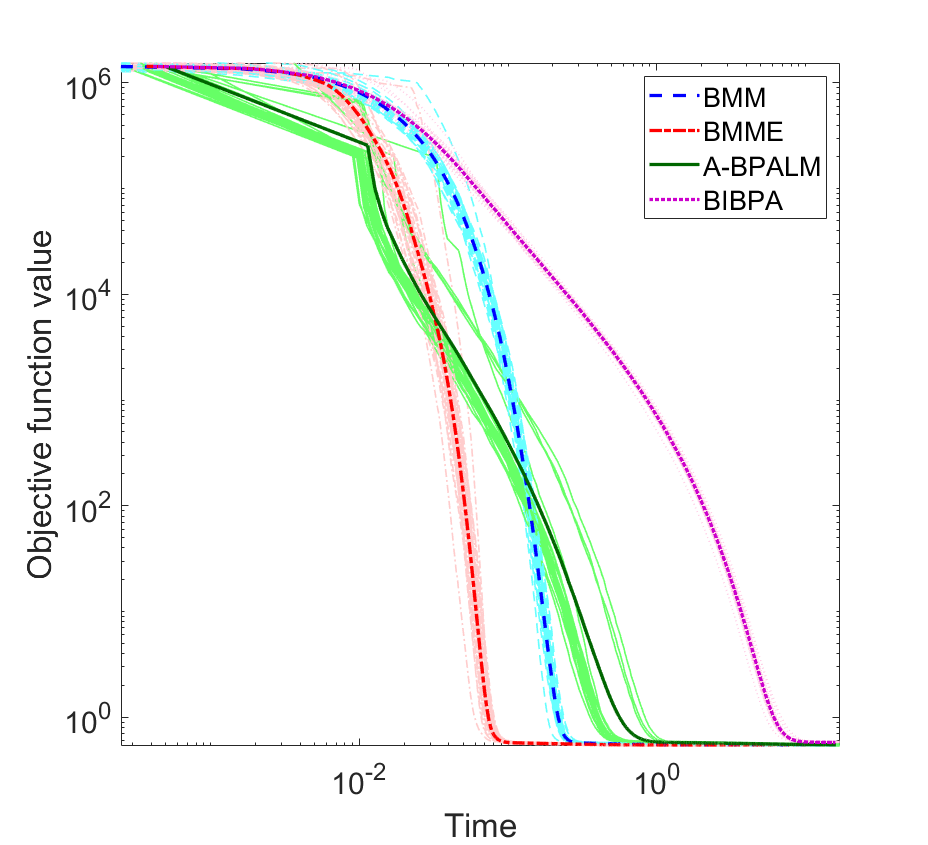
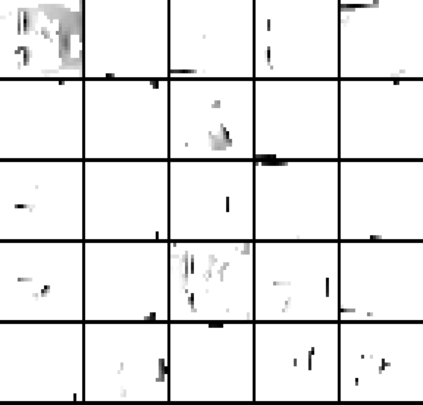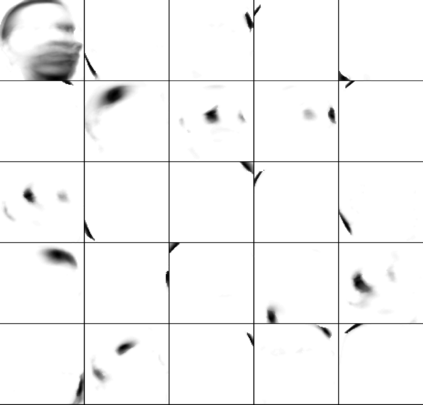In this paper, we consider a class of nonsmooth nonconvex optimization problems whose objective is the sum of a block relative smooth function and a proper and lower semicontinuous block separable function. Although the analysis of block proximal gradient (BPG) methods for the class of block $L$-smooth functions have been successfully extended to Bregman BPG methods that deal with the class of block relative smooth functions, accelerated Bregman BPG methods are scarce and challenging to design. Taking our inspiration from Nesterov-type acceleration and the majorization-minimization scheme, we propose a block alternating Bregman Majorization-Minimization framework with Extrapolation (BMME). We prove subsequential convergence of BMME to a first-order stationary point under mild assumptions, and study its global convergence under stronger conditions. We illustrate the effectiveness of BMME on the penalized orthogonal nonnegative matrix factorization problem.
翻译:在本文中,我们考虑的是一类非摩擦非convex优化问题,其目标在于块状相对平稳功能和适当和较低的半连续块分解功能之和。虽然对块状美元-smoth函数类别块状准梯度方法的分析已经成功地扩大到处理块状相对平稳功能类别的布雷格曼BPG方法,但加速的布雷格曼BPG方法稀少,难以设计。我们从Nesterov型加速和主要化-最小化计划中得到灵感,我们建议用外推法(BMME)建立一个块状交替布雷格曼主要化-最小化框架。我们证明BMME在轻度假设下随后与一阶固定点相融合,并在更强的条件下研究其全球趋同性。我们介绍了BMME在受惩罚的或多位非负式矩阵因子化问题上的有效性。