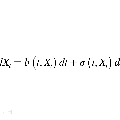This paper deals with the problem of efficient sampling from a stochastic differential equation, given the drift function and the diffusion matrix. The proposed approach leverages a recent model for probabilities \citep{rudi2021psd} (the positive semi-definite -- PSD model) from which it is possible to obtain independent and identically distributed (i.i.d.) samples at precision $\varepsilon$ with a cost that is $m^2 d \log(1/\varepsilon)$ where $m$ is the dimension of the model, $d$ the dimension of the space. The proposed approach consists in: first, computing the PSD model that satisfies the Fokker-Planck equation (or its fractional variant) associated with the SDE, up to error $\varepsilon$, and then sampling from the resulting PSD model. Assuming some regularity of the Fokker-Planck solution (i.e. $\beta$-times differentiability plus some geometric condition on its zeros) We obtain an algorithm that: (a) in the preparatory phase obtains a PSD model with L2 distance $\varepsilon$ from the solution of the equation, with a model of dimension $m = \varepsilon^{-(d+1)/(\beta-2s)} (\log(1/\varepsilon))^{d+1}$ where $0<s\leq1$ is the fractional power to the Laplacian, and total computational complexity of $O(m^{3.5} \log(1/\varepsilon))$ and then (b) for Fokker-Planck equation, it is able to produce i.i.d.\ samples with error $\varepsilon$ in Wasserstein-1 distance, with a cost that is $O(d \varepsilon^{-2(d+1)/\beta-2} \log(1/\varepsilon)^{2d+3})$ per sample. This means that, if the probability associated with the SDE is somewhat regular, i.e. $\beta \geq 4d+2$, then the algorithm requires $O(\varepsilon^{-0.88} \log(1/\varepsilon)^{4.5d})$ in the preparatory phase, and $O(\varepsilon^{-1/2}\log(1/\varepsilon)^{2d+2})$ for each sample. Our results suggest that as the true solution gets smoother, we can circumvent the curse of dimensionality without requiring any sort of convexity.
翻译:本文涉及从随机微分方程(SDE)中高效采样的问题,给定漂移函数和扩散矩阵。所提出的方法利用了最近的概率模型——PSD模型————可以在精度$\varepsilon$下获得独立同分布的(i.i.d)样本,成本为$m^2 d\log(1/ \varepsilon)$,其中 m 是模型的维度,d 是空间的维度。所提出的方法包括:首先计算满足SDE相关的Fock-Planck方程(或其分数变体)的PSD模型,误差为$\varepsilon$,然后从导出的PSD模型中采样。假设Fock-Planck解具有一定的正则性(即$\beta$阶可微加上一些其零点的几何条件),得到一个算法:(a)在准备阶段,获得满足方程解的L2距离为$\varepsilon$的PSD模型, ,其模型维数为$m=\varepsilon^{-(d+1)/(\beta-2s)}(\log(1/\varepsilon))^{d+1}$,总计算复杂性为$O(m^{3.5} \log(1/\varepsilon))$,然后(b) 对于 Fock-Planck方程,能够按照Wasserstein-1距离以误差$\varepsilon$生成i.i.d样本,每个采样的成本为 $O(d \varepsilon^{-2(d+1)/\beta-2} \log(1/\varepsilon)^{2d+3})$。这意味着,如果与SDE相关的概率具有一定的正则性,即$\beta \geq 4d+2$,则算法需要$O(\varepsilon^{-0.88} \log(1/\varepsilon)^{4.5d})$的准备阶段,并且每个采样需要$O(\varepsilon^{-1/2}\log(1/\varepsilon)^{2d+2})$。我们的结果表明,随着真实解的光滑度提高,我们可以规避维数灾难,而无需任何凸性。