Generalized Frank-Wolfe Algorithm for Bilevel Optimization

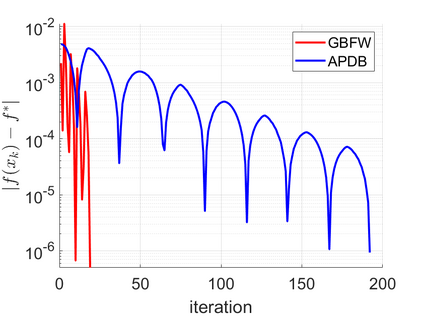
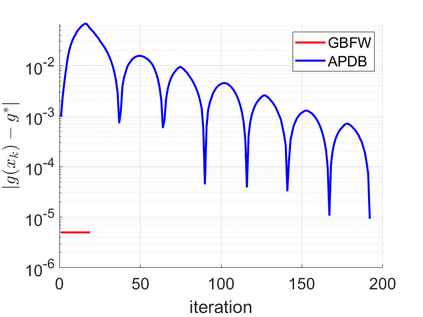
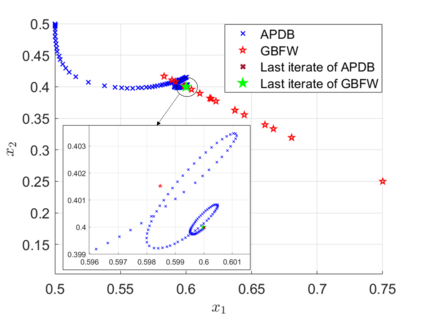
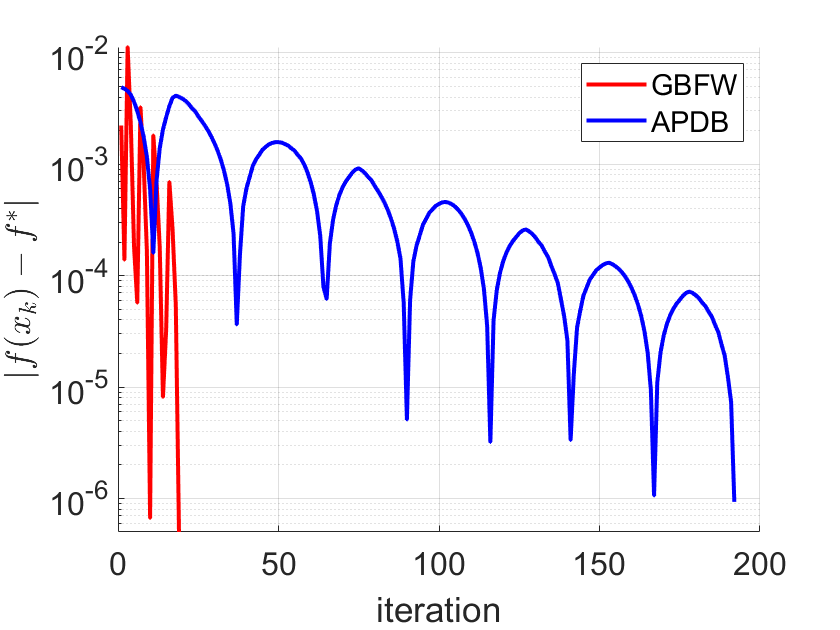
In this paper, we study a class of bilevel optimization problems, also known as simple bilevel optimization, where we minimize a smooth objective function over the optimal solution set of another convex constrained optimization problem. Several iterative methods have been developed for tackling this class of problems. Alas, their convergence guarantees are not satisfactory as they are either asymptotic for the upper-level objective, or the convergence rates are slow and sub-optimal. To address this issue, in this paper, we introduce a generalization of the Frank-Wolfe (FW) method to solve the considered problem. The main idea of our method is to locally approximate the solution set of the lower-level problem via a cutting plane, and then run a FW-type update to decrease the upper-level objective. When the upper-level objective is convex, we show that our method requires ${\mathcal{O}}(\max\{1/\epsilon_f,1/\epsilon_g\})$ iterations to find a solution that is $\epsilon_f$-optimal for the upper-level objective and $\epsilon_g$-optimal for the lower-level objective. Moreover, when the upper-level objective is non-convex, our method requires ${\mathcal{O}}(\max\{1/\epsilon_f^2,1/(\epsilon_f\epsilon_g)\})$ iterations to find an $(\epsilon_f,\epsilon_g)$-optimal solution. We further prove stronger convergence guarantees under the H\"olderian error bound assumption on the lower-level problem. To the best of our knowledge, our method achieves the best-known iteration complexity for the considered bilevel problem. We also present numerical experiments to showcase the superior performance of our method compared with state-of-the-art methods.