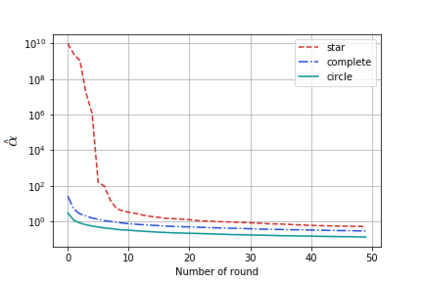
We introduce a new graphical bilinear bandit problem where a learner (or a \emph{central entity}) allocates arms to the nodes of a graph and observes for each edge a noisy bilinear reward representing the interaction between the two end nodes. We study the best arm identification problem in which the learner wants to find the graph allocation maximizing the sum of the bilinear rewards. By efficiently exploiting the geometry of this bandit problem, we propose a somehow \emph{decentralized} allocation strategy based on random sampling with theoretical guarantees. In particular, we characterize the influence of the graph structure (e.g. star, complete or circle) on the convergence rate and propose empirical experiments that confirm this dependency.
翻译:我们引入一个新的图形双线强盗问题, 即学习者( 或 \ emph{ 中央实体 ) 将手臂分配到图表的节点上, 并观察每个边缘的噪音双线性奖赏, 代表两个端节点之间的相互作用。 我们研究最好的手臂识别问题, 学习者想在其中找到图表分配方式, 使双线性奖赏之和最大化。 通过高效利用这个土匪问题的几何学, 我们提出了一个基于随机抽样的基于理论保证的 emph{ 分散化} 分配策略 。 特别是, 我们描述图表结构( 如恒星、 完整或圆形) 对汇合率的影响, 并提出证实这一依赖性的经验实验 。