Rebounding Bandits for Modeling Satiation Effects

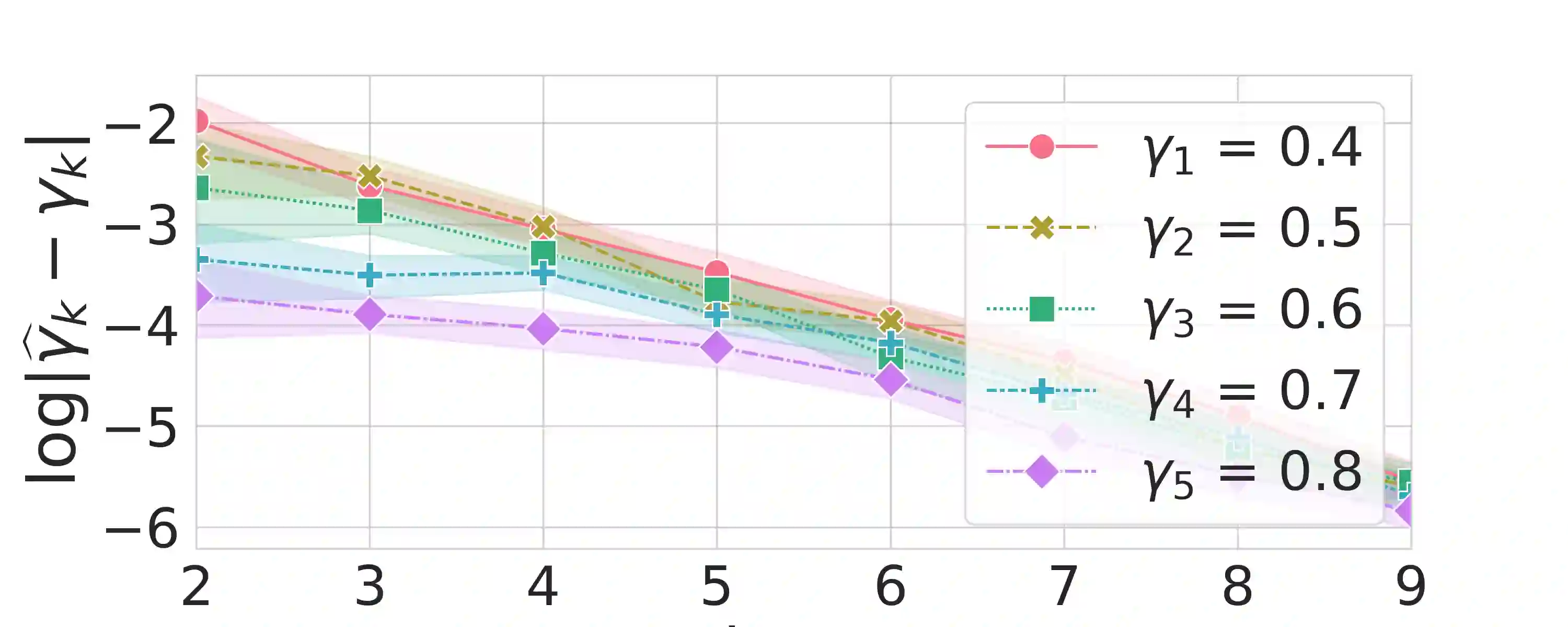
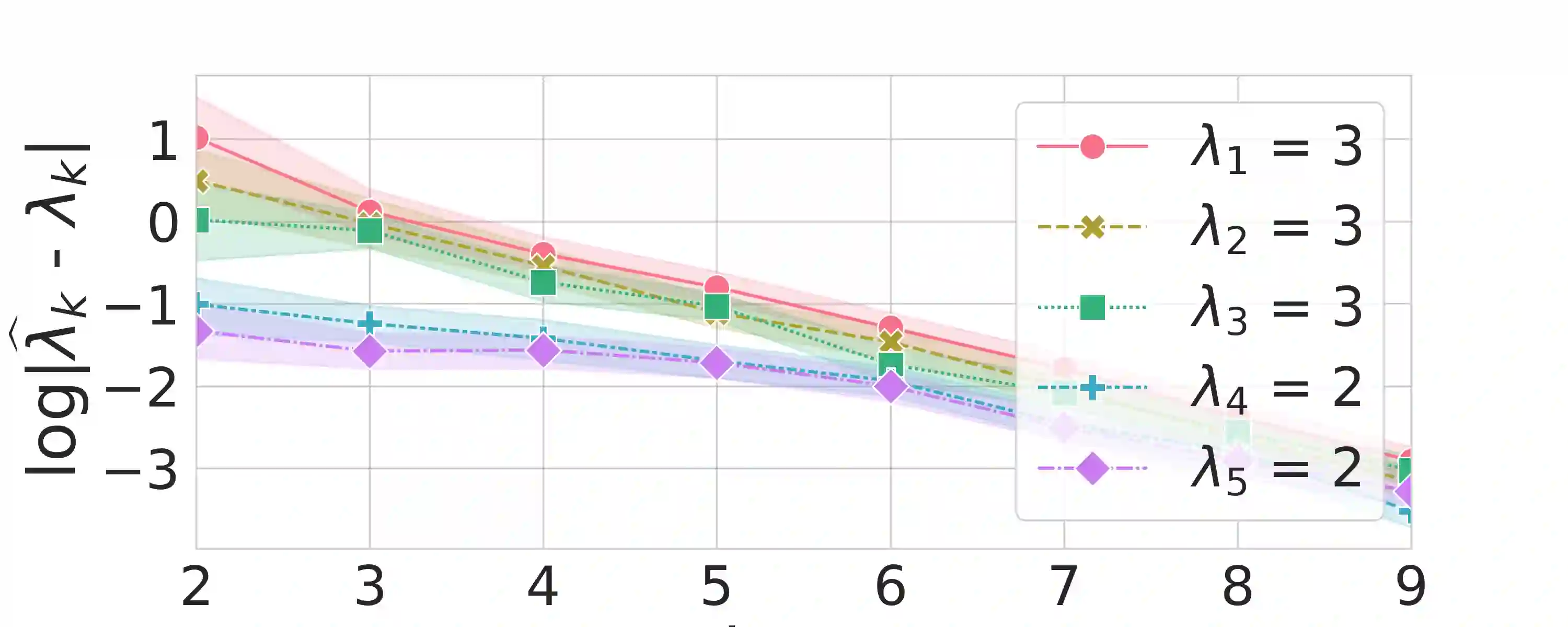
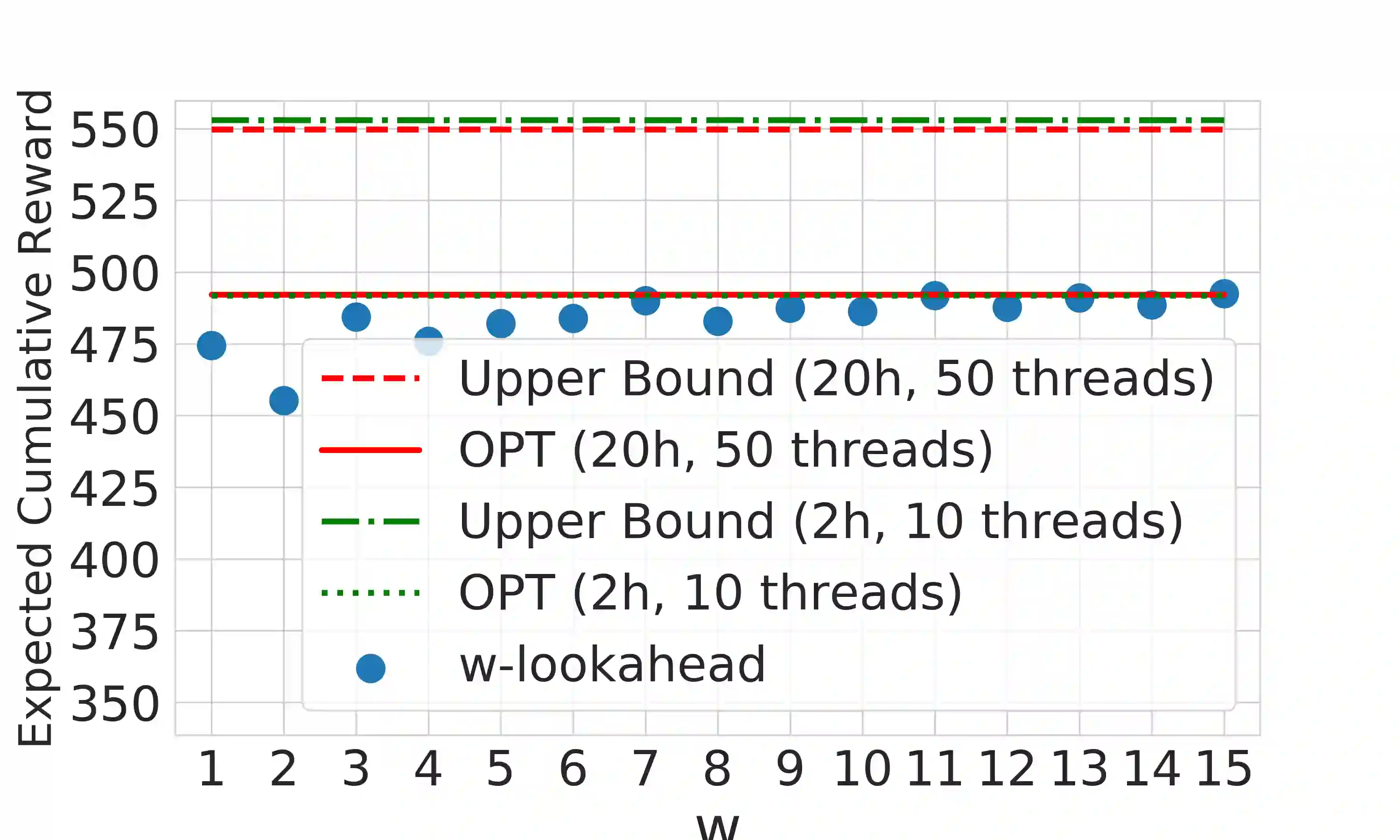
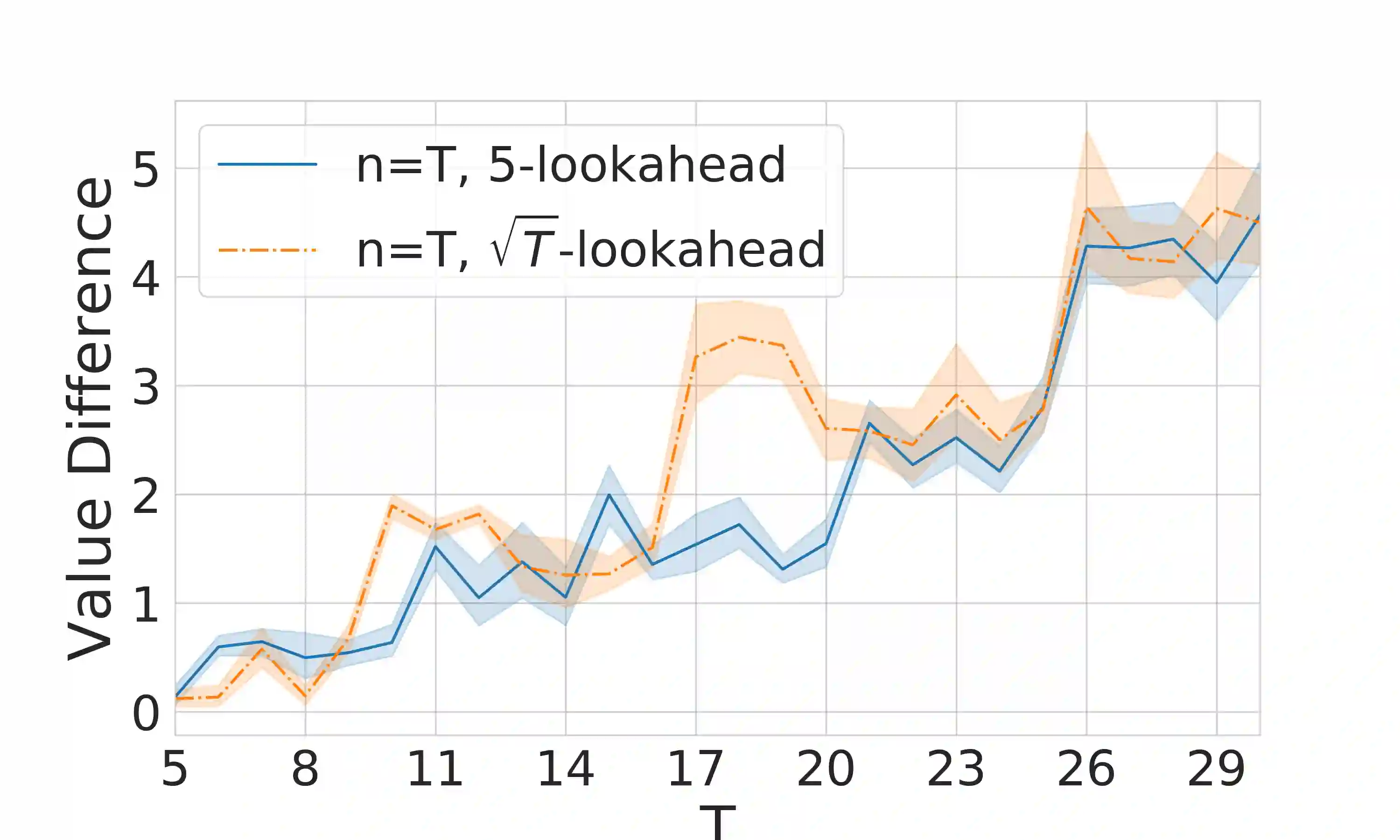
A large body of psychological research shows that enjoyment of many goods is subject to satiation, with short-term satisfaction declining after repeated exposures to the same item. Nevertheless, proposed algorithms for powering recommender systems seldom model these dynamics, instead proceeding as though user preferences were fixed in time. In this work, we adopt a multi-armed bandit setup, modeling satiation dynamics as a time-invariant linear dynamical system. In our model, the expected rewards for each arm decline monotonically with consecutive exposures to the same item and rebound towards the initial reward whenever that arm is not pulled. We analyze this model, showing that when the arms exhibit identical deterministic dynamics, our problem is equivalent to a specific instance of Max K-Cut. In this case, a greedy policy, which plays the arms in a cyclic order, is optimal. To handle the case when the parameters governing the satiation dynamics can vary across arms, we propose a lookahead policy that generalizes the greedy policy. When the satiation dynamics are stochastic and governed by different (unknown) parameters, we propose an algorithm that first uses offline data to identify an affine dynamical system specified by the reward model and then plans using the lookahead policy.